

Loading...
Global Optimization with no stepwise process!

Global Optimization with no stepwise process!
MiningMath software allows mining engineers to improve their strategic analysis through risk assessments that are unconstrained by a step-wise approach to optimization. MiningMath’s global mining optimization methodology helps to integrate multiple areas of the business. It handles all parameters simultaneously, delivering multiple scenarios and accounting for both strategic and tactical aspects.
Even the greatest engineers and algorithms might…

…miss opportunities, when one decision limits the next one.

MiningMath global mining optimization is not constrained by arbitrary decisions for cut-off grades or pushbacks. These decisions are usually guided by prior knowledge or automated trial-and-error. Thus, each set of constraints in our technology has the potential to deliver an entirely new project development. Along with the mine schedule, differences include economic, technical, and socio-environmental indicators, while aiming to maximize the project’s NPV.
The mining planning models that follow a step-wise methodology have developed shortcuts and approximations. These are made to enable the search for acceptable results that consider all the project’s complexities and constraints. Without these simplifications powerful machines are required to find a solution that simultaneously determines the optimum pit limit and mining sequence that delivers the maximum project value.
Below you can see a common stepwise approach to optimization.
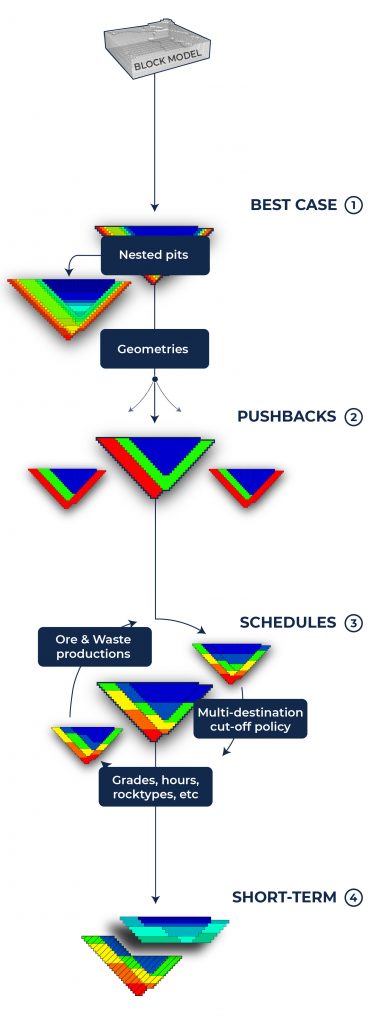
Representation of a step-wise approach from block model, nested pits, pushbacks, and schedules until short-term planning. Several strategies, algorithms or technologies can be employed in each step.
This step-wise approach is usually solved in three larger individual stages:
Nested pits: when finding nested pits, it's possible to employ the Lerchs-Grossmann (LG) algorithm, the Pseudoflow algorithm, direct block scheduling, more recent heuristic mechanisms or even consider more complex requirements such as destination optimization.
Pushback definition: having defined nested pits, the next step is to perform the definition of pushbacks. This can be done by some expert mine planning engineers using a number of empirical rules. Another approach could be through the use of automatic ways focused on NPV optimization for pushback design.
Schedules: finally, starting from a chosen pushback, the scheduling is performed. A myriad of techniques can be employed for that. For example, direct block scheduling, genetic algorithms, (fuzzy) clustering algorithms, dynamic programming, and heuristic methods in general. All with different rates of success, but limited variety of solutions due to the single pushback input.
Regardless of the technologies or algorithms, in a step-wise approach the aim is to initially find the final pit limit that maximizes the undiscounted cash flow, to then focus on block sequence within this final pit envelope. By splitting the problem and predefining inputs, these shortcuts (approximations) help to save time and computer resources. In turn, it is possible to consider complexities such as ore blending requirements, different processing routes, stockpiling policy, and others.
With the step-wise approach, thousands of potential schedules can be generated with a multitude of different methods. However, they all follow the same step-wise rationale, with one step guiding the next ones. Commonly, schedules follow from a set of nested pits and other fixed input parameters such as geotechnics, metallurgical performance, and blending constraints. Therefore, the results frequently present similar behaviors, restricting the full exploration of the solution space.
Your nested pits do not lead to feasible production plans?
Your pushbacks do not account for your blending needs?
Your short-term planning does not fit the long-term view?
Other geometric conditions could be tested for a better NPV?
Your cutoffs and sequence incur higher mining rates and stocks?
When using MiningMath’ global mining optimization, it is possible to define the pit limit and mine schedule simultaneously. That is, to determine which blocks should be mined, when this should happen and to where they should be sent to maximize the NPV. All that is made while respecting production and operational constraints, slope angles, discount rate, stockpiles, and so. Moreover, everything is performed in a single-step, straight from the block model. This means that the steps of pit optimization, pushback and scheduling are not obtained separately, but in a single, global and optimized process.
To help with the decision- making process, our software also allows you to build Decision Trees. These enable a broader view of your project and a deeper understanding of the impacts of each variable. This is all possible because MiningMath works with a global mining optimization that simultaneously regards all variables, instead of following a step-wise approach.
MiningMath acknowledges that each project has its own characteristics. Thus, it also allows you to choose which workflow fits best in your demand and decide which one should be used. For example, you could use it to define your Super Best Case for free. As MiningMath’s global mining optimization finds all periods simultaneously it has the potential to find higher NPVs. There is no need to use revenue factors. Hence, results are usually better when compared to traditional best case procedures based on LG/Pseudoflow nested pits, which do not account for processing capacities (gap problems), cutoff policy optimization and discount rate. Most commonly, these and many other real-life aspects are only accounted for later, through a stepwise process, limiting the potentials of the project.
MiningMath also offers the option of producing Optimized Pushbacks with controlled ore production and operational designs. Having this broader view in mind, you are already able to begin the scheduling stage, with Optimized Schedules. The block’s periods and destinations optimized by MiningMath could be imported back into your preferred mining package, for comparison, pushback design or scheduling purposes.
MiningMath provides different views and solutions for each parameter changed and each possible objective on the same mine, as depicted below.
Representation of the single-step approach employed by MiningMath, straight
from block model to short-term, schedules, optimized pushbacks or super best case.
Identify your bottlenecks before going into detailed planning
Check how each constraint interacts with each other
Test how each assumption impacts the economics
Search for realistic lower risk and higher potential scenarios
Reveal hundreds of unseen distinctive solutions!
Sure! Such unbelievable results are only possible due to MiningMath’s proprietary Math Programming Solver ©. It consists of a Mixed Integer Linear Programming (MILP) formulation and linearization methods that tackle the challenging non-linear aspects of the mining optimization. It also has its own Branch & Cut algorithm fine-tuned to this specific optimization problem and able to provide more efficiency than standard MILP optimizers.
Another major advantage of MiningMath comes from the mathematical formulations based on surfaces (Goodwin et al., 2006; Marinho, 2013), instead of usual block precedence. Block precedence methods might lead to higher errors (Beretta and Marinho, 2014), providing steeper slopes (i.e. riskier, more optimistic) than requested. The use of surfaces eliminates geotechnical errors and allows for block-by-block geotechnical zones, if needed. They also allow MiningMath to include geometric constraints and, consequently, find solutions that are closer to real mining operations. You can guide geometries by including mining and bottom widths, mining lengths, maximum vertical advance rates, and forcing/restricting mining areas. Such constraints give freedom for you to work, or not, with predefined cut-offs and pushbacks which might limit the space of potential solutions.
All that is explained in our Knowledge Base, while you can also use our forums to interact with the community and have any questions answered. MiningMath’s approach has been applied for years by our customers, with an increasing number of licenses sold worldwide, press releases and academic research also proving the consistency of the implementation.


With constant developments since 2013, MiningMath has reached a mature and robust state, providing solutions straight from the block model. It is the first and only single-step mining optimization engine available in the market!
MiningMath’s approach. From block model to schedule in a single step solved by its proprietary Math Programming Solver ©.
Windows 64-Bit (x86_64) - 121 MB
Hi, it's Mima here 😇 Ask me any questions!