Azimuth Rotation Procedure

Estimated reading: 2 minutes 236 views

MiningMath supports the use of block models that have been rotated using an Azimuth rotation.

Rotation steps

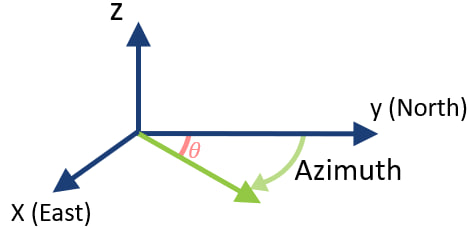
This procedure performs a rotation of a point around a specific origin in the \(XY\) plane, while preserving the \(Z\) coordinate. Below are the steps involved, along with the corresponding mathematical formulas.

Azimuth normalization
First, the azimuth value is adjusted to ensure it lies within the range of \(0\) to \(360\) degrees. This is done by taking the remainder of the azimuth divided by \(360\)
\(\text{azimuth} = \text{fmod}(\text{azimuth}, 360.0)\)
In mathematics, the function \(\text{fmod}\) (floating-point modulus) computes the remainder of the division of two floating-point numbers. If the azimuth value is negative, \(360\) degrees is added to make it positive:
\(\text{azimuth} = \begin{cases}
\text{azimuth} + 360.0 & \text{if } \text{azimuth} < 0.0 \\
\text{azimuth} & \text{otherwise}
\end{cases}\)
Inversion of Rotation Direction
The adjusted azimuth is then inverted to perform the rotation in the opposite direction:
\(\text{azimuth} = -\text{azimuth}\)
Conversion from Degrees to Radians
The azimuth in degrees is converted to radians, as trigonometric functions use radians:
\(\text{radians} = \frac{\text{azimuth} \times \pi}{180.0}\)
Calculation of New Coordinates
The new \(x\) and \(y\) coordinates are calculated by applying the rotation in the \(XY\) plane around an origin \((x_0, y_0)\). The formulas used are:
\(
p_x = \left( (x - x_0) \times \cos(\text{radians}) + (y - y_0) \times \sin(\text{radians}) \right) + x_0\)
\(
p_y = \left( -(x - x_0) \times \sin(\text{radians}) + (y - y_0) \times \cos(\text{radians}) \right) + y_0\)
Where \((x, y)\) are the initial coordinates of the point, and \((x_0, y_0)\) are the coordinates of the origin.
Preservation of Z Coordinate
The \(z\) coordinate of the original point remains unchanged during the rotation:
\(z_{\text{final}} = z_{\text{initial}}\)
Final Result
The result of the procedure is a new point with coordinates \((p_x, p_y, z)\), where \(p_x\) and \(p_y\) are the new coordinates in the \(XY\) plane after the rotation, and \(z\) is the original coordinate in the \(Z\) axis.
\(\text{New Point} = \{ p_x, p_y, z \}\)

MiningMath

Loading...

Azimuth Rotation Procedure

Rotation steps

CONTENTS