Loading...

Math Optimization models that integrate multiple business’ areas

Our Plans
Updated on November 18, 2024

Widths and lengths

Estimated reading: 4 minutes 2093 views

On MiningMath, the widths and lengths are constraints within the objective function, which means that they are regarded in the optimization instead of being considered just on the pit design stage, when roads, access are drawn to conceive an operational feasible to the pit.

The definition of minimum widths is a pretty useful feature to obtain operational results and play with different geometries accordingly with the project requirements. It is important to understand that they are very complex parameters to be respected while considering 3-dimensional non-linear models, which also influence the runtime of each scenario. Therefore, it is not possible to always guarantee that all minimum widths are respected due to the deposit geometry and also the constraints hierarchy. Testing different values is a great strategy to identify opportunities that could bring the best mining sequence and NPV.

Types of widths and legnths

Bottom widths

Bottom widths (BW) are the minimum horizontal distance, on the lowest floor of the pit, as seen in Figure 1. It is required to allow mining operations based on the equipment sizing. This parameter is considered the same for all periods and is related to adjacent slopes and applicable in other areas regarded as pit bottoms.

Figure 1: Bottom width area in subsequent periods

Mining widths

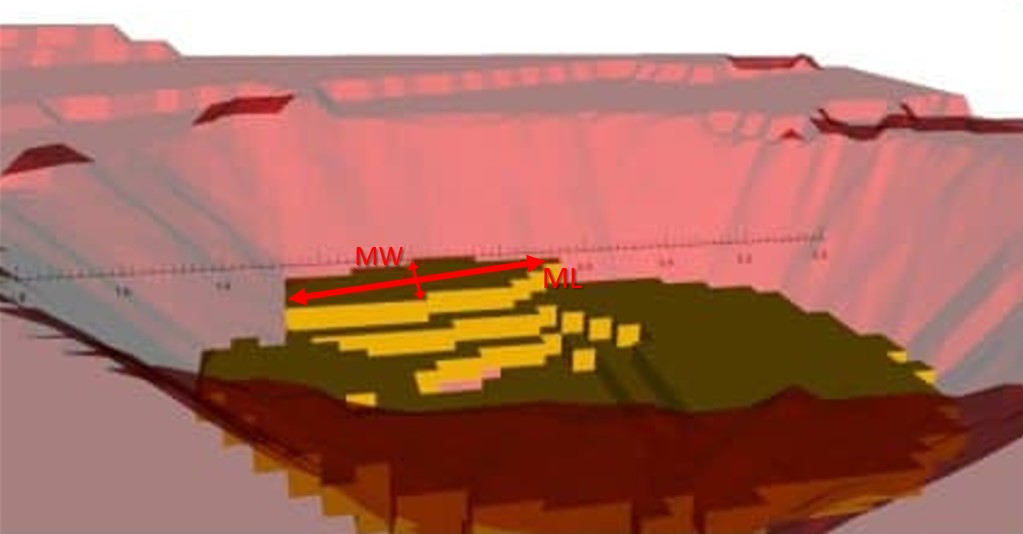
Mining widths (MW) are the minimum horizontal distance that should be respected from a pit to another in every period, which means that this is the horizontal distance between the walls of two surfaces that belonged to consecutive periods, as shown in Figure 2.

This feature is more complex than the minimum bottom width since it would drastically change the pit shapes to identify the best regions. Note that wider values provide greater mining fronts and also better designs to nested pits, pushbacks, schedules, or any other result that you are looking for.

Figure 2: Mining width in subsequent periods

Mining lengths

The Mining Length (ML) represents a minimum distance that must exist between at least two points amidst the walls of surfaces among two consecutive mining periods. This distance is already respected for any values smaller or equal to the MW. Thus, this parameter extends such distance between any two points for a value greater than MW. Figure 3 depicts an example

Imagem da mina
Figure 3: Example of MW and ML.

Identifying geometric parameters

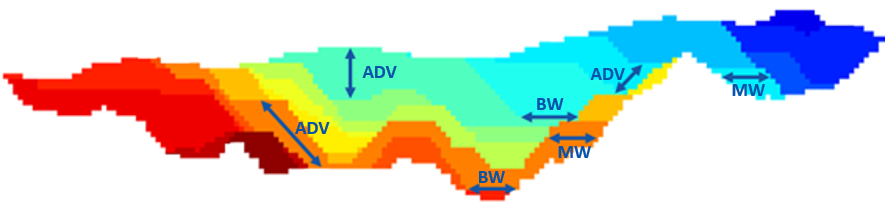
Figure 4 shows a section view of the McLaughlin deposit, where each color represents a given period. The horizontal arrows highlight the bottom and the mining width, while others identify the vertical advance. Mining lengths cannot be depicted in this 2D representation.

Figure 4: Bottom width, Mining width and vertical rate of advance.

How are widths defined?

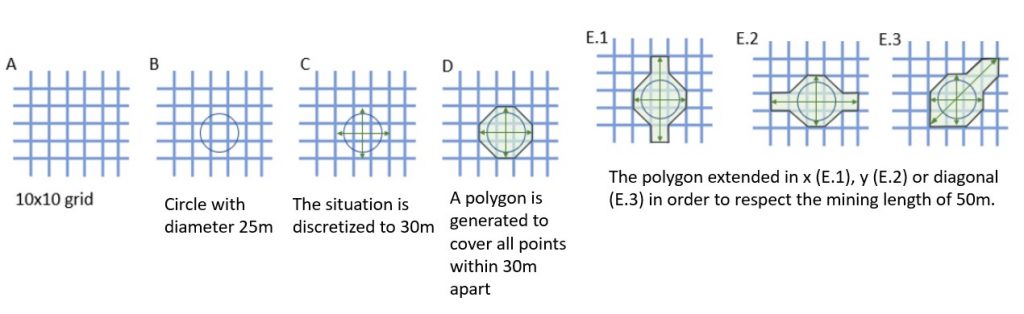
The widths inputted in the interface define a diameter (d) of a circle. As MiningMath does not mine partial blocks, the software will consider the block size as a reference to define whether d should be rounded up to the next integer multiple. The approximated circle results in a polygon, whose objective is to select centroids of adjacent cells. Then, MiningMath will assign the same elevation value to the selected cells to define mining surfaces.

Figure 5 shows, in sequence, an example of how the minimum width of 25 meters and possible mining length of 50 meters could be defined over a 10 x 10 meters grid (block’s dimension in x and y direction).

Figure 5: How MiningMath defines the mining width and mining length.
Geometry - Previous Geometric Constraints Next - Geometry Vertical Rate
Share this Doc

Widths and lengths

Or copy link

CONTENTS
Chat Icon

Hi, it's Mima here 😇 Ask me any questions!