Current Best Practices
MiningMath software allows mining engineers to improve their strategic analysis through risk assessments performed in a single-step approach to optimization. In other words, MiningMath’s global mining optimization methodology helps to integrate multiple areas of the business. It handles all parameters simultaneously, delivering multiple scenarios and accounting for both strategic and tactical aspects.
Hence, it is important to understand other current best practices employing a stepwise rationale and their disadvantages compared to MiningMath’s single-step approach.
Stepwise technologies
The mining planning models built with current best practices have developed shortcuts and approximations to try to deliver acceptable results that consider all the project’s complexities and constraints. To handle it, powerful machines are required to find a solution and to simultaneously determine the optimum pit limit and mining sequence that deliver the maximum project value.
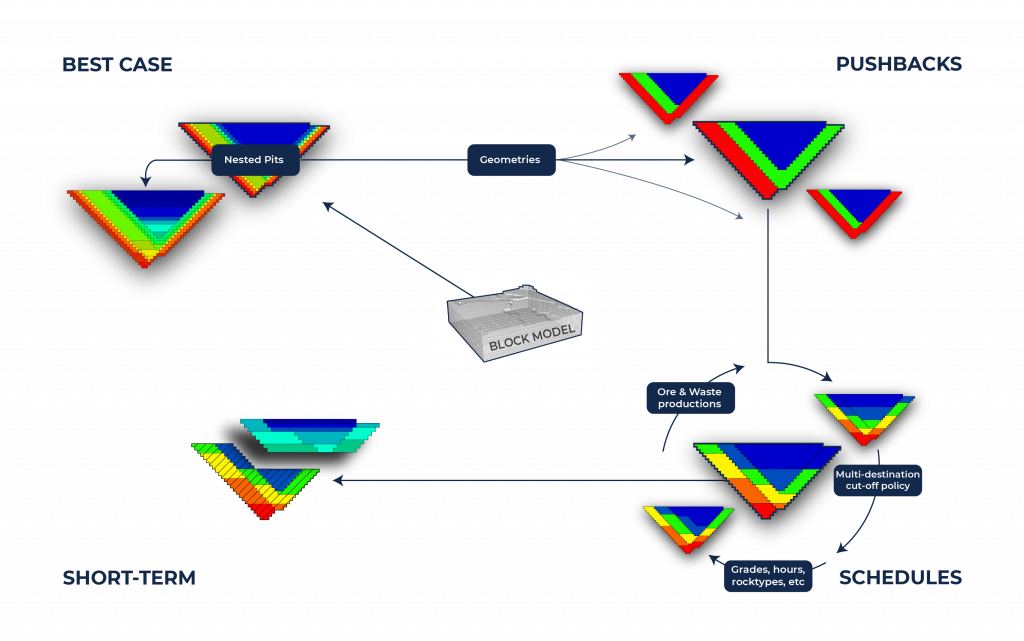
Figure 1 depicts a stepwise approach used by current best practices.
Figure 1: Current best practices: stepwise approach
Stages of stepwise approaches
These steps may include different strategies, technologies or algorithms. However, they are all usually solved individually in three larger stages:
- Nested pits: when finding nested pits it is possible to employ the Lerchs-Grossmann (LG) algorithm, the Pseudoflow algorithm, destination optimization, direct block scheduling, or even more recent heuristic mechanisms.
- Pushback definition: having the nested pits defined, the next step would usually be to perform the definition of pushbacks in a manual way by some expert mine planning engineers using a number of empirical rules. Automatic ways focused on NPV optimization could also be employed for pushback design, but these are usually under resource constraints and do not consider enough geometric requirements.
- Schedules: finally, starting from a chosen pushback, the scheduling is performed. A myriad of techniques can be employed for that, such as direct block scheduling, genetic algorithms, (fuzzy) clustering algorithms, dynamic programming, and heuristic methods in general. All with different rates of success, but limited variety of solutions due to the single pushback input.
Aim of stepwise approaches
Regardless of the technologies or algorithms, in a stepwise approach the aim is to initially find the final pit limit that maximizes the undiscounted cash flow to then focus on block sequence within this final pit envelope. By constraining the problem and predefining inputs, these shortcuts (approximations) help to save time and computer resources, enabling such software to consider complexities such as ore blending requirements, different processing routes, stockpiling policy, truck fleet considerations, and so on.
Disadvantages of stepwise approaches
With current best practices employing some stepwise approach, thousands of potential schedules can be generated with a multitude of different methods, but they are all based on the same stepwise rationale, with one step guiding the other. Commonly, schedules follow from a set of nested pits and other fixed input parameters such as geotechnics, metallurgical performance, blending constraints, etc. Therefore, the results frequently present similar behaviours and restrict the full exploration of the solution space.
MiningMath Solution
MiningMath solves the stepwise issues through math optimization models that integrate multiple areas of the business, in a single-step. It handles all parameters simultaneously and delivers multiple scenarios, accounting for both strategic and tactical aspects. To better understand MiningMath uniqueness please continue reading here.