Loading...

One of the unavoidable steps for the next generation of Data Science and Artificial Intelligence technologies applied to mining

Our Plans
Updated on November 18, 2024

Discounted vs. Undiscounted Cash Flow

Estimated reading: 4 minutes 500 views

MiningMath’s objective function maximizes the discounted cash flow over the entire life of the mine in a single mathematical optimization step, taking all necessary constraints into account simultaneously. In contrast, other software packages that use LG/Pseudoflow methods for pit optimization focus on maximizing the undiscounted cash flow for each given revenue factor. Hence, the solutions provided by MiningMath are not easily comparable to undiscounted flow approaches that only consider slope angles.

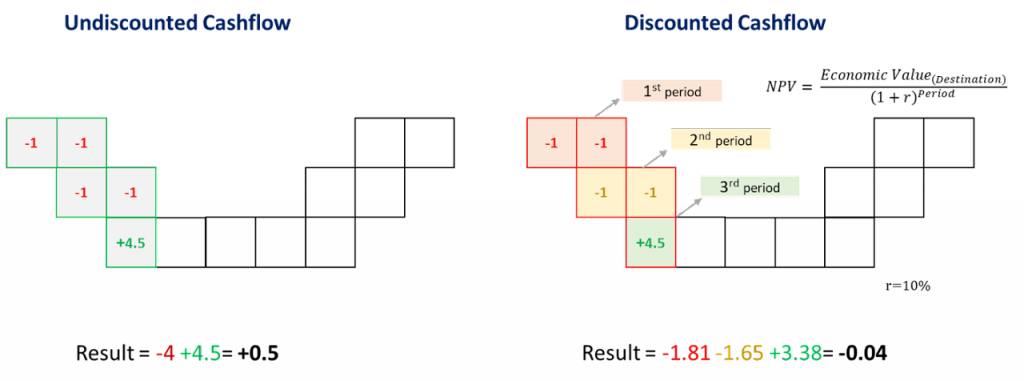
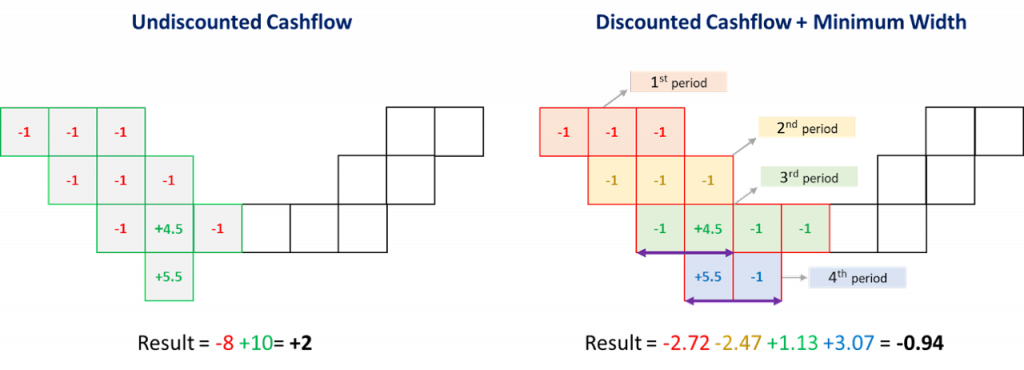
A visual comparison between undiscounted and discounted cash flows is provided below. This comparison indicates that MiningMath’s decision not to mine certain regions is likely due to the higher cost of waste removal outweighing the potential profit from extracting hidden ore. Despite discounting, the revenue from the hidden ore is insufficient to cover the extraction costs in these areas.

Example of discounted and undiscounted cashflow
Undiscounted versus discounted cash flow optimization.
Undiscounted versus discounted cash flow optimization regarding a minimum mining width.

Comparing the different methodologies​

A proper comparison between both methodologies could be done if you import the final pit surface obtained from the other mining package into MiningMath, and use it as Force/Restrict mining. By utilizing this surface as a guide, MiningMath can precisely optimize scheduling within the specific boundaries delineated by the imported surface. This integration simplifies the comparison of NPV between MiningMath and various other mining packages, giving a more comprehensive evaluation of the methodologies employed by each one.

For comparisons targeting specific objectives, such as maximizing early-period cash flow or identifying profitable areas in the initial years, the following examples will guide you in setting up the appropriate scenarios within MiningMath.

Cash flow in the early periods

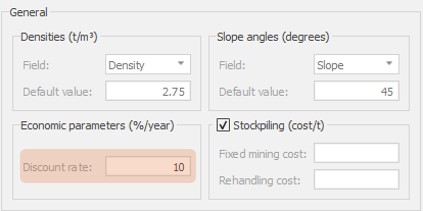
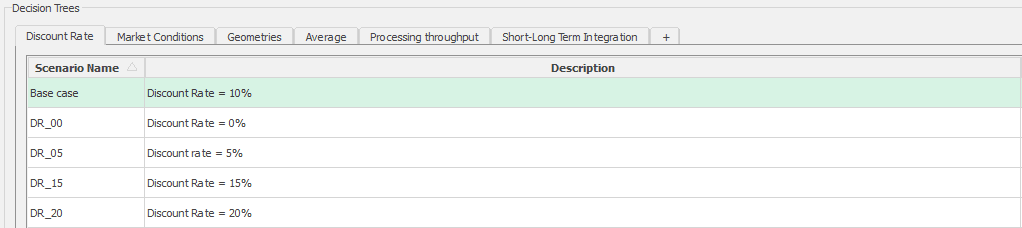
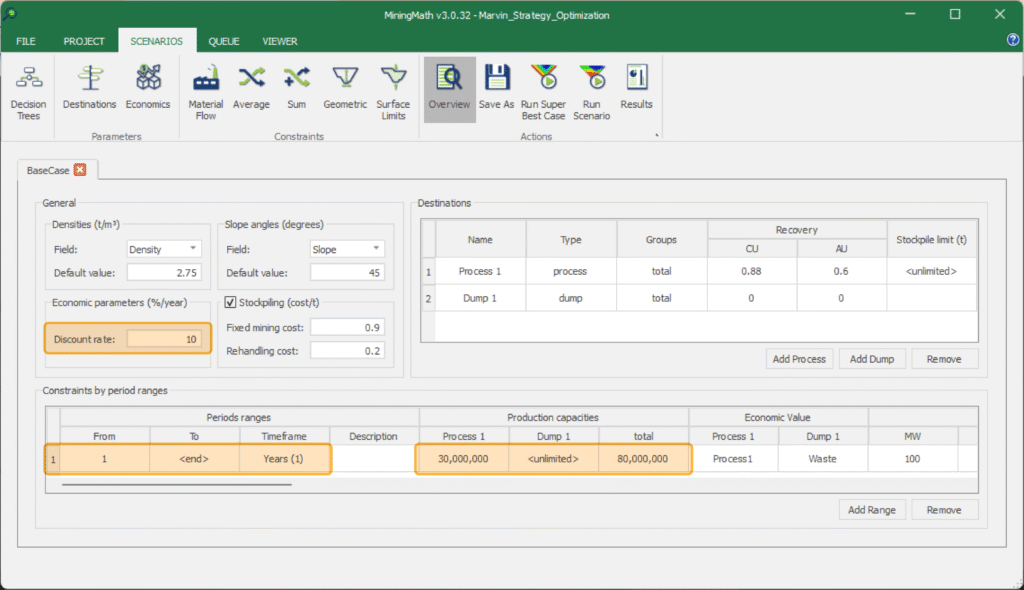
If you want to emphasize the cash flow in the early mining periods, simply create a decision tree varying the discount rate. The higher the rate value, the more weight will be given to the early periods, leading the undiscounted cash flow to have higher values at the beginning, while later periods will be heavily penalized by the discount rate.

Discount rate field.
Custom decision tree with scenarios employing different discount rates.

Greedy behavior as in the context of nested pits

If you wish to mimic the same greedy behavior as in the context of nested pits in MiningMath, you should drop all constraints and set a 1-<end> (only) interval with the desired ore productions, asking MiningMath to focus solely on maximizing the cash flow of this single pit, regardless of the long-term consequences, as in the picture below and similar to this process.

Focusing on finding the most profitable area during the early years

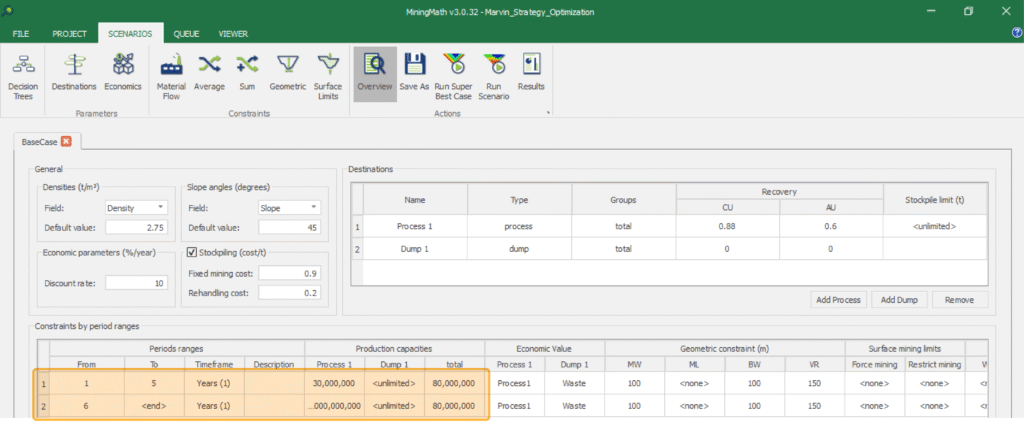
If you with to focus on finding the most profitable area to operate during the early years and the long-term consequences of such decisions are not an immediate concern, you must setup MiningMath accordingly., dropping all constraints after initial years. For example, it is possible to only have interval 1-5 timeframe (represensint the first 5 years) and 6-<end> with no constraints and infinite productions, as depecited below.

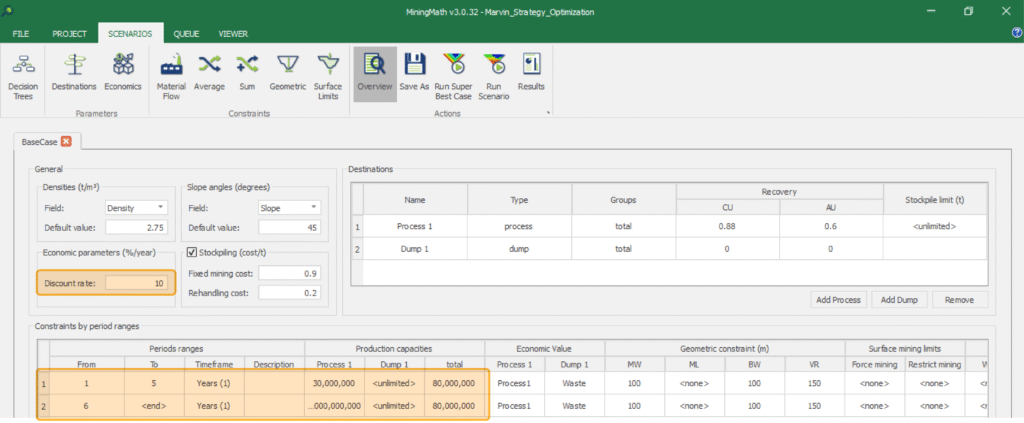
An even greedier approach would be to have just the 1-5 interval, meaning “I only have these 5 years to operate this mine”. In this case, you could also setup the discount rate to zero, so that you can analise only the undiscounted cashflow.

MiningMath allows you to keep as much of the global view as you wish while constraining your project as much as needed, even changing criteria for short and long-terms. If you’re unsure, simply run multiple scenarios and choose the one that best meets your objectives.

General Content - Previous Predefined Destinations Next - General Content Azimuth Rotation Procedure
Share this Doc

Discounted vs. Undiscounted Cash Flow

Or copy link

CONTENTS
Chat Icon

Hi, it's Mima here 😇 Ask me any questions!