Geometric Constraints
In a mining project, the mine planner must accurately dimension each unit operation to determine the most suitable set of equipment for the existing conditions. With MiningMath, operational parameters are integrated as constraints within the objective function, rather than being applied post-pit optimization. This methodology ensures solutions that adhere to operational criteria while maximizing NPV, leading to more effective data utilization and uncovering opportunities that might be overlooked with manual steps and arbitrary assumptions.
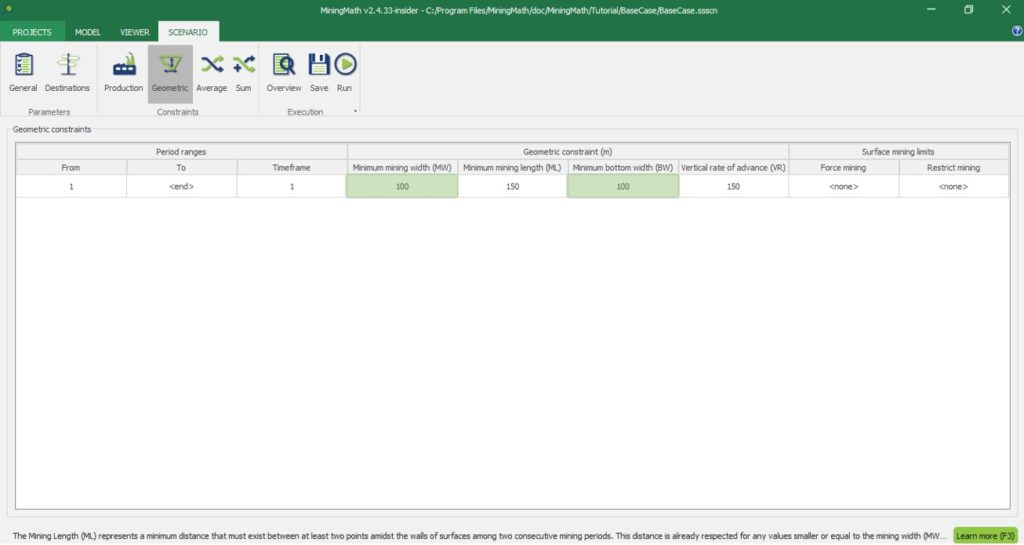
The Geometric tab is the place to set minimum mining & bottom widths, mining length and vertical rate of advance, whose values are applicable to every period. The user can also use surfaces to define operational constraints in compliance with period ranges, which can limit, force or achieve an exact shape, based o the constraints hierarchy.
There are two types of widths restrictions that can be created:
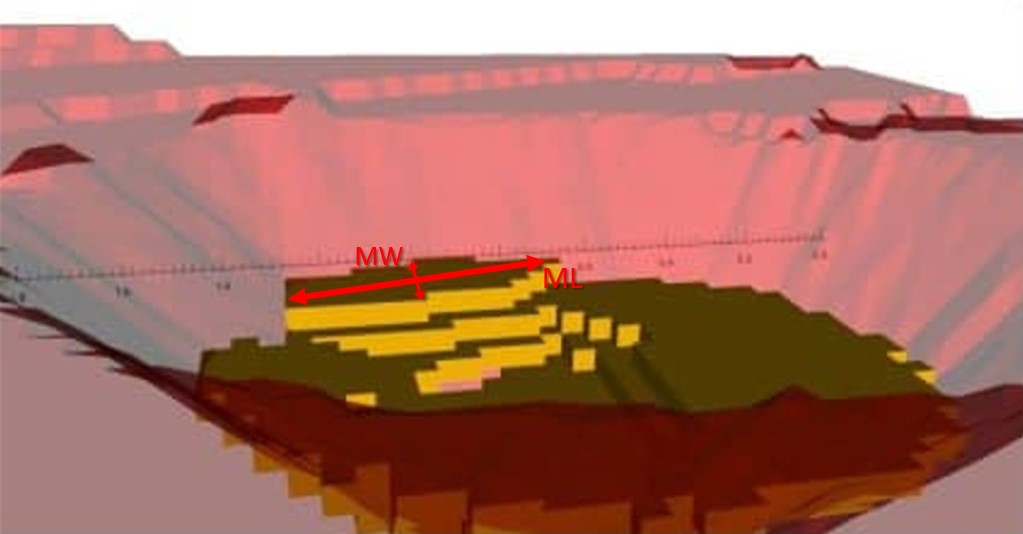
Mining Width: distance from a pit to another.
Bottom Width: bottom minimum area.
Currently, MiningMath does not mine partial blocks. As a consequence, the software will round up any widths to cover the next integer block.
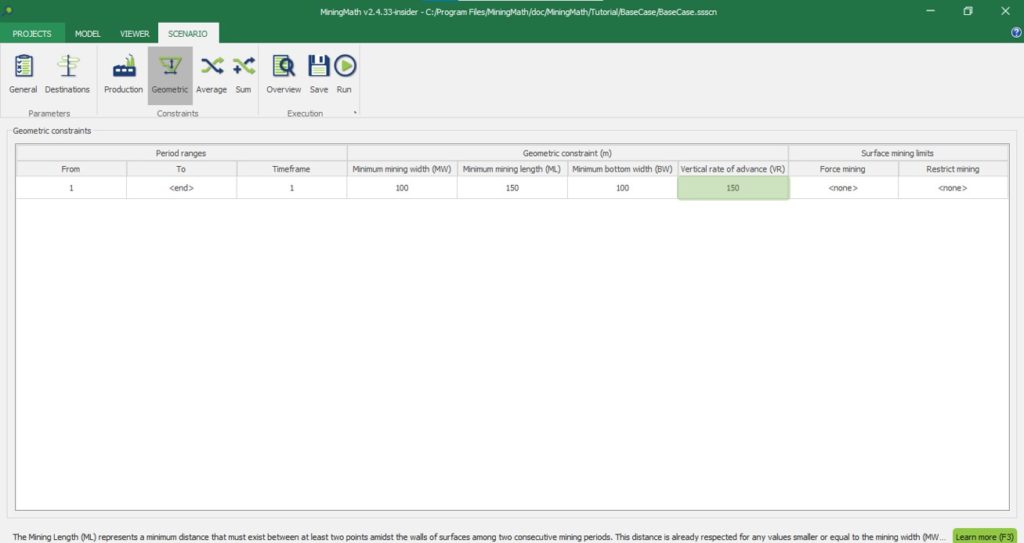
It is also possible to define a Vertical Rate of Advance for each period range. The VR will be rounded up to cover the next integer block.
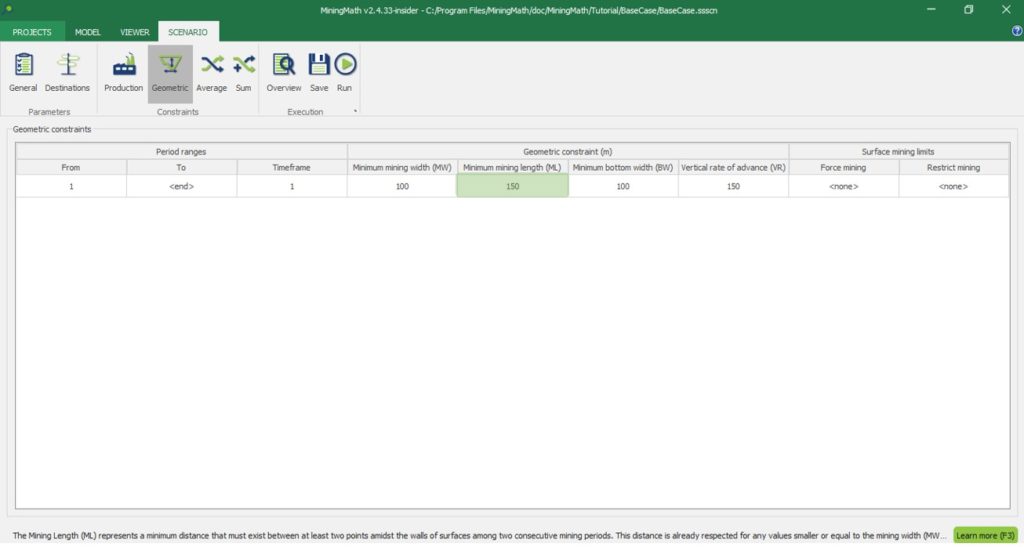
Mining length (ML)
A minimum horizontal distance that should be respected from a pit to another in every period can also be defined in the Minimum Mining Length field. Currently, this is only available in the insider version.
The figures below show a simplistic meaning of each width/length available and the vertical rate of advance.
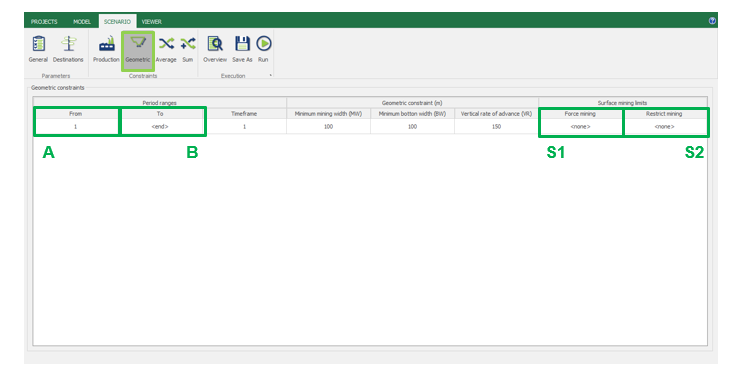
For each period range, the user can consider:
1 force mining surface.
1 restrict mining surface.
Each surface file is valid from period A up to final of period B, as depicted below.
The following video shows how the variation of operational constraints impacts your solution and how you can take advantage of these parameters to find results more closer to the reality.
Operational constraints
