Optimization Hints

Estimated reading: 5 minutes 1451 views

Impact of constraints on NPV optimization

The relationship between the number of constraints and Net Present Value (NPV) is generally inversely proportional. Scenarios with fewer constraints enable the optimization algorithm to search more freely, often leading to higher NPV results. It is therefore recommended to first explore the full potential of a mining project, starting with the Data Validation procedure, followed by the other possible Workflows that can inform further steps.

A study on constraint impacts

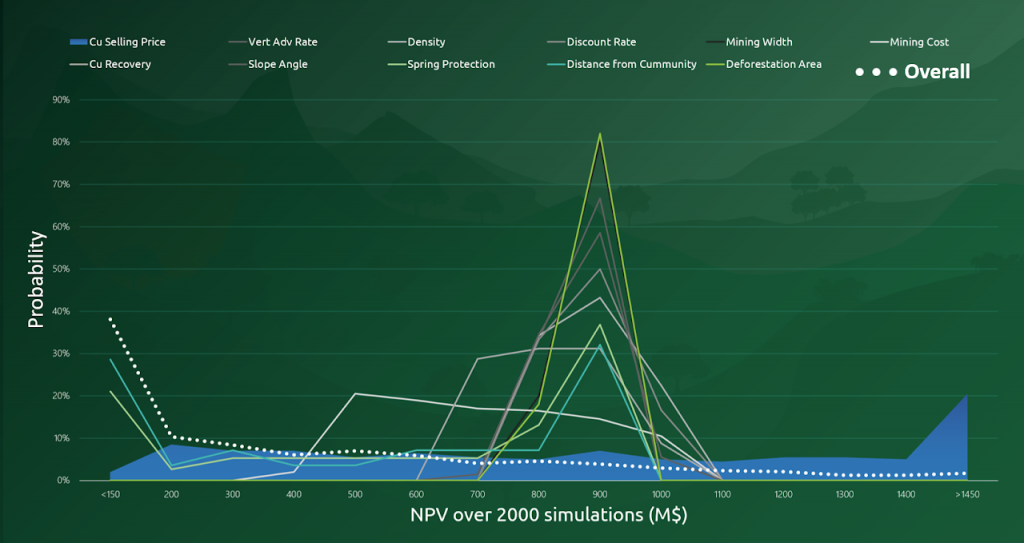
To better understand the effects of constraints, the MiningMath team conducted 2,000 simulations as depicted below.

The study examined the impact of both individual constraints and their combined effects.

Individual Variation
Initial simulations tested the effect of varying individual constraints such as Copper Selling Price, Mining Widths, and Vertical Rate of Advance. These parameters were adjusted individually to understand their tendencies. The results showed that most individual variations had a high probability of generating NPVs around $900M.
Combined Scenarios
The next phase involved running "overall" scenarios, where all 11 variables were assigned random values simultaneously. In these cases, the constraints collectively reduced the NPV potential, with a higher likelihood of NPVs around $200M.

Balancing freedom and constraints

The findings of the above study highlight a key principle: increasing constraints tends to decrease the likelihood of achieving higher NPVs. Users are encouraged to explore constraints to strike a balance between freedom for the algorithm and guidance to achieve practical results. Some strategies for that are given throughout the page.

The trade-off between constraints and NPV

Too many constraints: Limits the algorithm’s ability to explore the solution space, leading to lower NPVs.
Too few constraints: Provides excessive freedom, which can result in impractical solutions for real-life scenarios.

Insights into MiningMath's algorithm

MiningMath employs mathematical programming to maximize NPV while respecting imposed constraints.

Advanced users can take advantage of this capability by strategically placing constraints that guide the optimizer toward better solutions.

For example, starting with unrestricted total movement/production allows for better waste distribution over time. Subsequently, applying production limits (e.g., 100 Mtpa, 90 Mtpa) helps assess tendencies by creating a curve of scenarios against NPV.

Constraint management

The ideal approach begins with minimal constraints and gradually introduces reasonable ones. By doing so, the algorithm focuses on a narrower solution space, potentially yielding higher NPVs.

Recommended workflow

Start with minimal constraints and avoid adding complex geometries.
Gradually introduce constraints one by one to observe their impact on NPV.
Use an Workflow to assess how each assumption influences long-term project outcomes.
Measure the "cost" of each constraint to guide managerial decisions.

Smart constraint strategies

Relax constraints when possible: For instance, temporarily flex slope angles to improve designs.
Use hints to guide the algorithm: Relax low-priority constraints or simplify complex scenarios into smaller problems.
Iterate gradually: Optimize from the least-constrained to the most-constrained scenarios.

Shake-up approach

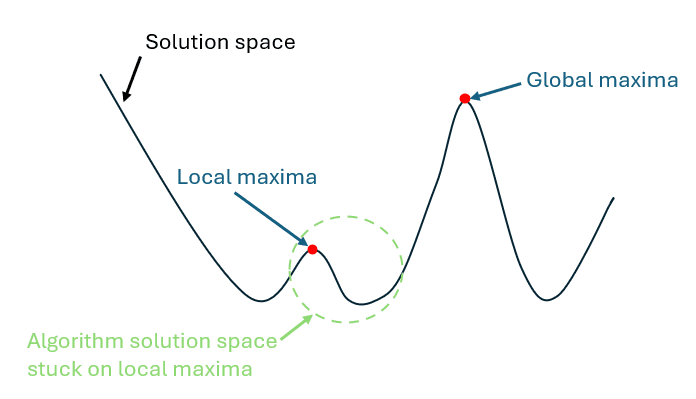
Nonlinear optimization problems often present challenges due to the presence of local maxima, where the algorithm may become “stuck,” preventing it from finding the global maxima.

One effective strategy to mitigate this issue is to introduce slight modifications to the parameters. These adjustments should be small enough that they do not significantly alter the practical outcome but are sufficient to change the mathematical structure of the problem.

Some examples (not exhaustive) of constraints that could be shaked-up are:

Processing Capacities: Introduce minor changes to processing limits. For example, reducing or increasing the mill capacity by 1-2% can shift the balance between waste handling and ore processing priorities.
Discount Rate: Slightly tweak the discount rate used in NPV calculations. This affects how future revenues are valued and can lead the algorithm to favor different project schedules.
Stockpile Parameters: Change the maximum or minimum limits for stockpiling by small amounts. This can prompt the algorithm to explore alternative stockpiling strategies.
Time limit: It is possible to indicate a time limit in hours before running a scenario. Despite not being implemented for this purpose, this parameter might also be used to find more diverse solutions.

This “Shake-up” approach encourages the algorithm to explore alternative paths in the solution space, potentially bypassing local maxima and improving the chances of identifying better solutions.

Relaxed vs. violated constraints

Understanding the nuances of constraints is critical. Constraints may be relaxed to achieve feasible outcomes but should not be violated in ways that render the project unfeasible.

Examples of constraints that could be relaxed:

Processing stream shortfalls.
Operational constraints.
Certain average or sum-based constraints (depending on the deviation).

Examples of violated constraints

Production limits exceeded.
Slope angle violations.
Critical average or sum-based constraints that breach feasibility.

Reports detailing these nuances are available in the Excel output’s Report Tab for review.

Key takeaways!

Explore freedom first: Begin optimization with minimal constraints to discover the economic potential of a project.
Introduce guidance gradually: Add constraints thoughtfully to guide the algorithm toward realistic results.
Leverage hierarchy: Use the hierarchy order to prioritize and relax constraints strategically.
Iterative problem-solving: Break down complex scenarios and iterate over multiple runs to assess tendencies.
“Shake-up” approach: Slightly modify your parameters to encourage the algorithm to explore alternative solutions.

MiningMath

Loading...