Cut-Off Grades

Estimated reading: 6 minutes 2673 views

MiningMath and cut-off grades!

MiningMath does not rely on predefined assumptions for determining a limit for cut-off grades. Instead, it uses mathematical optimization based on discounted cash flow while considering various constraints such as production capacity, blending, and vertical advances. Unlike traditional methods, it is not limited by fixed pits, pushbacks, or phases; the mining sequence is an optimized result based on the input parameters. This flexibility is especially beneficial in complex cases with multiple destinations or constraints, helping to uncover hidden opportunities.

Definition

The cut-off grade is the concentration of a mineral or metal required to classify material as either ore or waste. Material with a concentration above the cut-off is classifed as ore, while anything below is classified as waste.

Different from MiningMath, other software packages usually make manual assumptions to pre-define a cut-off, and based solely on that, decide whether some material should be processed or not. That is needed, for example, before running LG or Pseudoflow algorithms. However, this simplified approach doesn’t account for other required mine scheduling constraints. Moreover, even the best algorithms commercially available for destination optimization perform this task apart from mine scheduling.

How MiningMath operates

MiningMath is not constrained by cut-off grades, fixed pits, or pushbacks. It’s the only software available that optimizes the mining sequence and the destination optimization in a single-step, all at once, considering the all constraints applied, as a truly global optimization process.

These advantages become even more apparent in more complex cases with multiple destinations or constraints that could be overlooked, hiding potentially valuable opportunities when not considered jointly.

As a result, MiningMath may reveal new possibilities, deliver more realistic results and even lead to an increase in NPV through its unique single-step optimization.

Since the algorithm does not employ cut-offs to manually assign destinations to blocks, it automatically sends the less valuable blocks to the dump, based on the constraints you’ve set. MiningMath prioritizes meeting all constraints to optimize the average grade, leading to an increase in NPV through global optimization. Hence, even blocks with positive economic value may be discarded if their value is below the minimum required for processing at a given time. In scenarios without stockpiling policies, blocks with higher positive value may also be sent to waste, as there’s no alternative destination. As a result, MiningMath may deliver outcomes different from your initial expectations. However, for comparative purposes you can adjust the results as needed using the methods suggested below.

Are you not a MiningMath user?

With MiningMath’s single-step, optimization engine, you can uncover opportunities that manual or stepwise planning might miss. Ultimately, its engine is able to optimize resource utilization and can improve project outcomes. Transform your mine planning process by leveraging MiningMath’s advantages and take your mining projects to new heights of efficiency and success.

Forcing cut-off grades (not recommended)

Forcing a cut-off grade on MiningMath will likely make you lose part of the advantages it can offer. However, for many reasons, mining professionals might still be willing to force it, either to compare different methodologies, to understand the practical effects of using it or not, and so on. Different approaches are available to force a cut-off grade, which are described next. Note that these could also be employed to forbid any material type on the plant.

Using predefined destinations

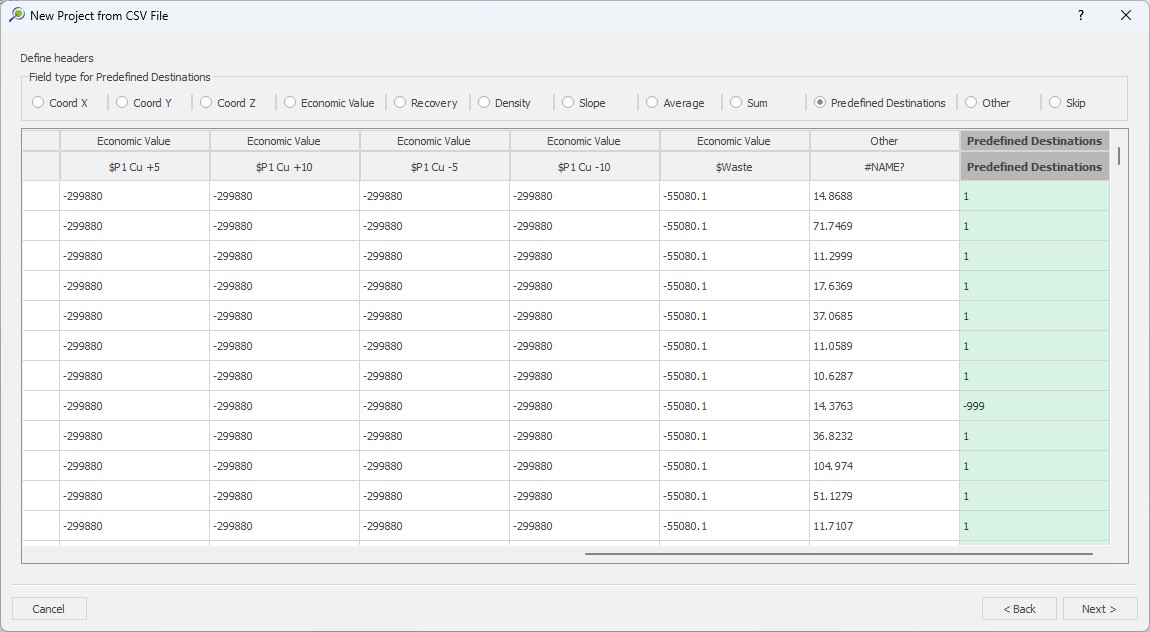
Predefining destinations before any optimization is performed is also a possibility within MiningMath when importing a block model.

A detailed guide on how to use this parameter can be seen here.

Using Economic Values

You can create multiple columns of economic values, each one for a cut-off you want to test. Then, force MiningMath to use this limit by defining very negative values for the destination you want to avoid, as depicted below, for a cut-off of 0.5. The math is:

Economic Value Process = If [Ore_Grade] > [0.5], then [f(Economic Value)], else [-999,999,999.00]

Using Average tab

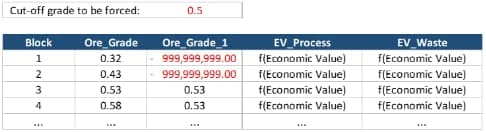
Grades in MiningMath are controlled as a minimum and/or maximum average calculation, which means that these limits do not represent cut-off values since the algorithm can use lower values to blend higher ones. Thus, to use this approach, just set a very negative value on the grades below the cut-off so that these blocks would reduce substantially the average when processed. It can also work to constraint a contaminant maximum limit by adding a high grade on it, as it can be seen below. Once again, the math is:

Ore_Grade1 = If [Ore_Grade] < [0.5], then [-999,999,999.00], else [Ore_Grade]

Using Sum tab

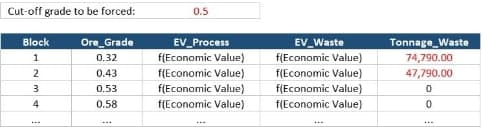
Another option is by using the sum tab to control material types. Therefore, it would be required to create a field to calculate only waste blocks mass and set the constraint of the maximum limit of it in the plant as zero, as it can be seen below. It is worth mentioning that this approach could increase the complexity of the optimization due to the priority order within the algorithm.

Tonnage_Waste = If [Ore_Grade] < [0.5], then [Volume*density], else [0]

Understanding results

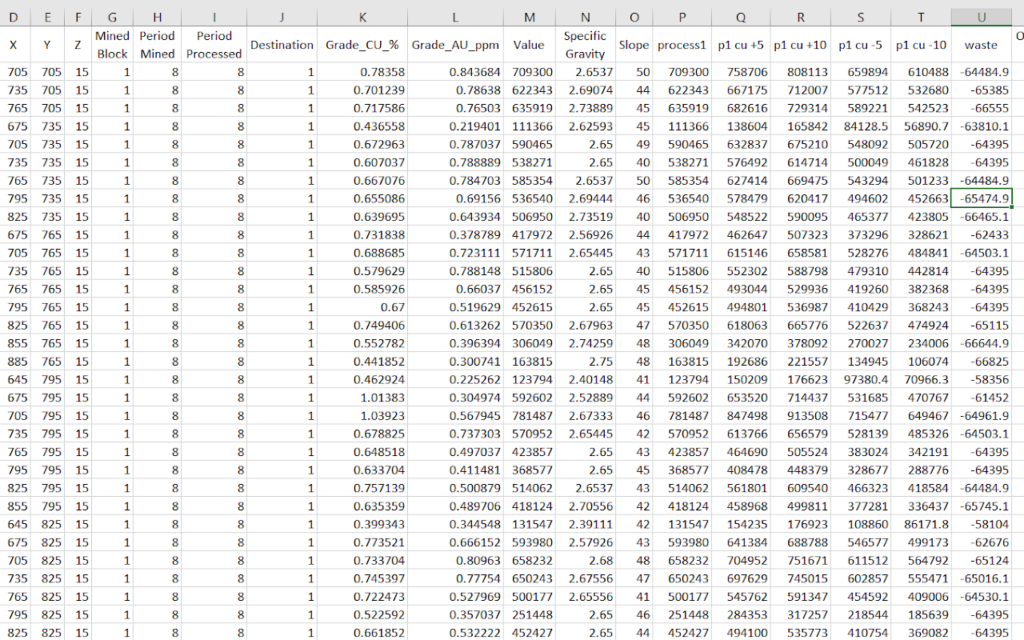
The mined blocks file (example below) is the main output to trace the blocks from each destination, to understand the results, and to find the best way to enhance your reporting based on any detail that you wish to disclose.

There are many useful tips to identify, and understand the results generated, some of them, are listed below:

Filter results where the period mined is equal to the period processed (blocks processed). Check the process economic values of those blocks and identify the lower one (which means the cut-off value at the plant). This can be compared with higher processing economic value of those who went to the dump.
Calculate the average grade of any material in period mined equal to the period processed filter. Check if the blocks going to dump would have exceeded any limit in the plant. If so, even having good economic values, they would not comprise the constraints in place.

To sum up, there are a lot of validations that can be done to understand why the algorithm is taking such decisions. It is also worth mentioning that any constraint can influence the results, even geometric ones, which could change the sequence and also change the destination of a block at any period.

MiningMath

Loading...