Slope Angles
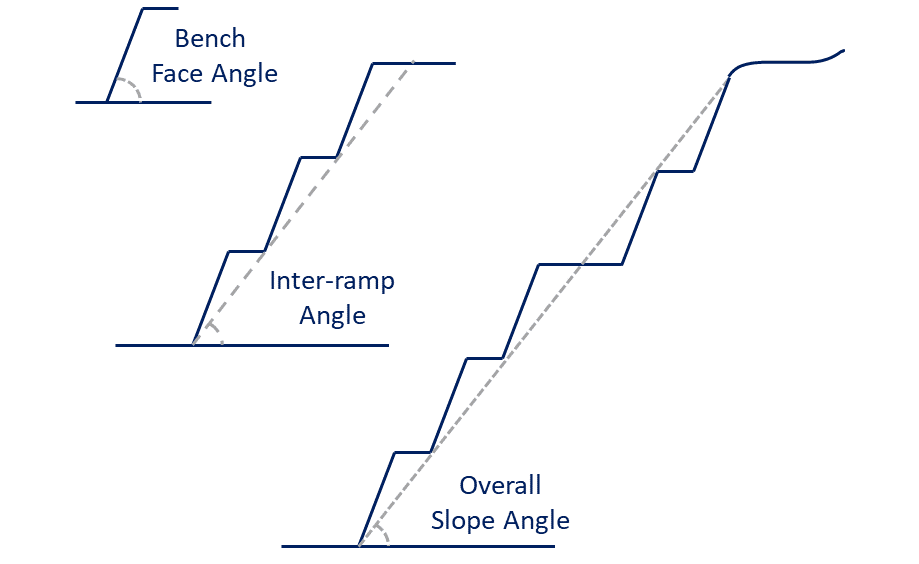
Slope angles are a critical consideration in the mining industry, as they directly impact safety and significantly influence a wide range of operational parameters. The most relevant types include:
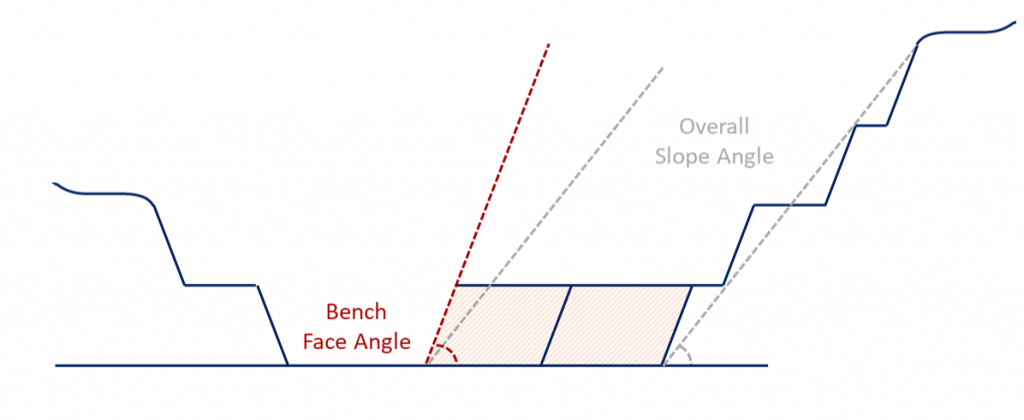
- Bench face angle (BFA): The angle between the vertical and the bench slope face, measured within an individual bench.
- Inter-ramp angle: The angle measured between the toe of the bottom bench and the crest of the top bench, encompassing multiple benches but excluding ramps or haul roads.
- Overall slope angle (OSA): The angle measured from the bottom-most point of the pit to the top-most point, incorporating all benches, ramps, and haul roads.
Each of which plays a specific role in balancing safety, operational efficiency, and ore recovery. This makes slope angles one of the most critical parameters when establishing a constraints hierarchy. Their values often vary depending on factors such as time frames (short- or long-term), rock type, lithology, mine sector, depth, and geotechnical domains. Therefore, it is essential to clearly define these assumptions to use this parameter effectively and align it with your project’s specific goals.
Are you not a MiningMath user?
With MiningMath’s single-step, optimization engine, you can uncover opportunities that manual or stepwise planning might miss. Ultimately, its engine is able to optimize resource utilization and can improve project outcomes. Transform your mine planning process by leveraging MiningMath’s advantages and take your mining projects to new heights of efficiency and success.
Discrepancies between optimization and design phases
The traditional workflow for open-pit optimization, design, and production scheduling often leads to discrepancies between the parameters used during the optimization phase and those applied during the design phase. Ramp design and placement, for instance, significantly influence the OSA, creating a mismatch. This misalignment frequently necessitates an iterative process of re-optimizing the same scenario based on the finalized pit design.
How MiningMath works
MiningMath controls the Overall Slope Angle through a “surface-constrained production scheduling” approach, where surfaces define groups of blocks to be mined (or not), instead of relying on the traditional “block precedence” method. This approach enables MiningMath to incorporate geometric constraints into its unique single-step optimization, delivering solutions that are closer to real mining operations.
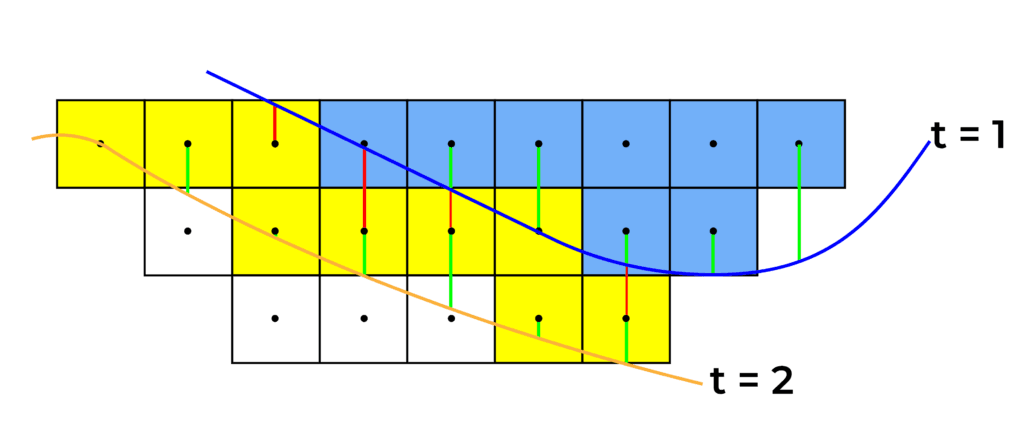
Timing of block extraction
Surfaces determine the timing of block extraction. For instance, blocks located between the surfaces associated with periods 1 and 2 will be mined in period 2. A block is considered “between” two surfaces if its centroid lies within the vertical space defined by them. In this example, blue blocks are mined in period 1, while yellow blocks are mined in period 2.
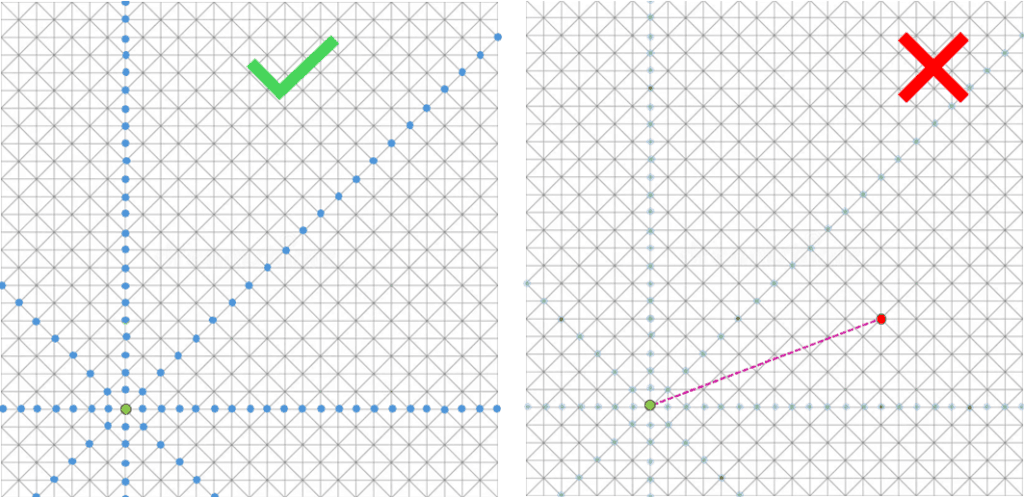
Grid-base approach for controlling slope angles
Within surfaces, slope constraints are managed by controlling the angles between adjacent points within a defined grid structure, rather than evaluating the angles between arbitrary pairs of points, as depicted below.
MiningMath employs a continuous linear variable for slope control, achieving superior accuracy compared to the discrete nature of block-based methods. Moreover, this grid-based approach ensures precise approximation of the deposit’s angles by focusing exclusively on grid-connected points, eliminating the need for comparisons between unrelated points. Adjacent elevations within a single surface must comply with a maximum allowable height difference, calculated based on the specified slope angle restriction (read more). This method guarantees that each generated surface represents a feasible solution while adhering to production requirements and delivering enhanced accuracy, particularly in transition zones.
Computational complexity
While it is theoretically possible to analyze more pairs of points that are not adjacent, such an approach would result in a significant increase in computational complexity. Both our practical experience and academic research (here and here), demonstrate that this added effort is not justified. MiningMath’s method already delivers more precise slope control than traditional precedence-based techniques.
Technologies based on Lerchs-Grossmann/Pseudoflow!
Unlike MiningMath, technologies based on the Lerchs-Grossmann and Pseudoflow approaches often exhibit a well-known “slope error”, which represents the discrepancy between the input parameters for the OSA and the actual measurements derived from the output pit shells. This issue arises from the “block precedence” methodology, where calculations connect the block’s centroids, a process that may not align with the block model dimensions. As a result, the decision to mine a block in its entirety or not can impact the OSA, potentially complicating the generation of a pit shell that matches the designed pit.
Setting up slope angles
MiningMath provides two options for handling slope angles:
Block-specific slope definitions directly within the model.
A default slope value that can be applied universally or used as a fallback for blocks without predefined slope information.
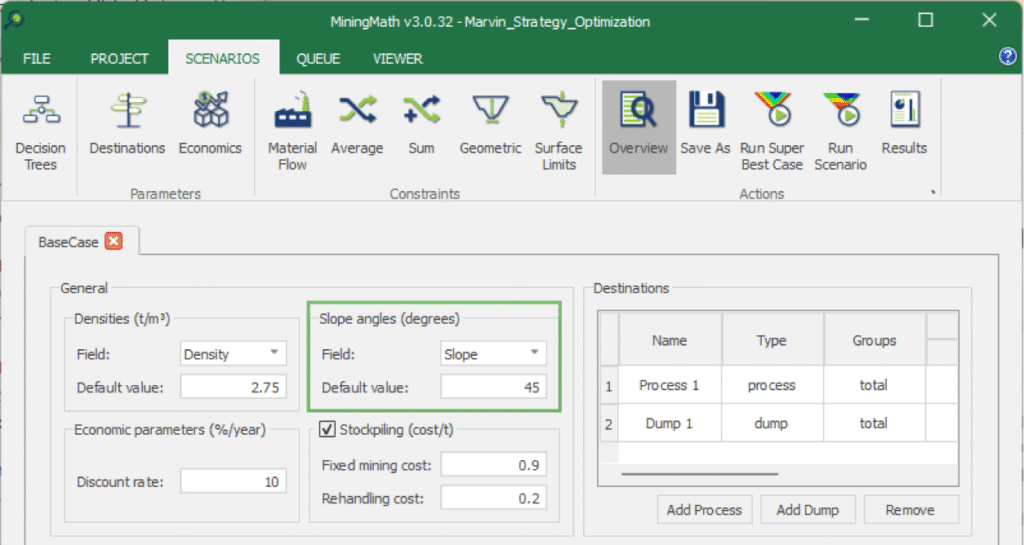
In the interface, these can be found in the General tab.
For scenarios requiring multiple variable slope assumptions, you can prepare additional columns (e.g., Slope 1, Slope 2, … Slope N) in the block model before import. This setup allows you to select the appropriate slope data for each scenario directly through the interface, eliminating the need to repeatedly edit and re-import the block model.
Default values
In the interface, you can choose the field option as the primary rule for variable slope angles or select <none> to apply a constant value across the entire model. If the chosen field contains missing data, the defined default value will automatically be used for those blocks.
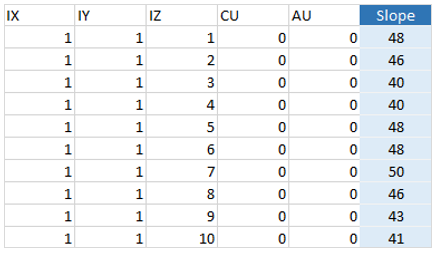
Block by block field
When assigning a field to the slope angles parameter, this will represent the column that will be assigned to the slope on each block as depicted below.
This approach allows a high level of flexibility to use any specific criteria. These possibilities can also comprise bi-dimensional and tri-dimensional variations, beyond linear and non-linear functions.
Employing slope angles in the short-term
Short-term planning presents a valuable opportunity to leverage the same platform used by the strategic mine planning team, enhancing project adherence and reconciliation. By selecting a surface and applying it as a constraint, mining can be restricted to specific areas, refining the entire operation.
This approach can utilize a surface already designed with ramps or any surface generated by MiningMath that adheres to the OSA within the required time frame.
This flexibility allows for steeper Bench Face Angles based on operational blasting parameters. To maximize this feature, follow the suggestion to set up angles block by block and experiment with different angles according to your project’s capabilities. This methodology enables the algorithm to adjust the constraints hierarchy, ultimately leading to improved results.
