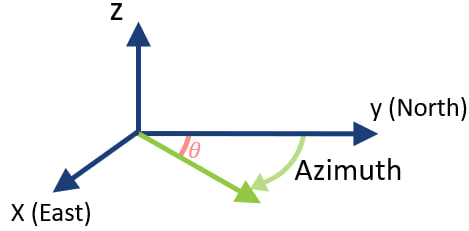
Procedimiento de rotación de acimut
MiningMath admite el uso de modelos de bloques que se han rotado mediante un Azimut rotación.
Pasos de rotación
Este procedimiento realiza una rotación de un punto alrededor de un origen específico en el \(XY) avión, mientras se preserva la \(Z) coordinar. A continuación se detallan los pasos a seguir., junto con las fórmulas matemáticas correspondientes.
Normalización del acimut
Primero, El valor del acimut se ajusta para garantizar que se encuentre dentro del rango de \(0\) para \(360\) grados. Esto se hace tomando el resto del azimut dividido por \(360\)
\(\texto{azimut} = \text{modo f}(\texto{azimut}, 360.0)\)
En matemáticas, La función \(\texto{modo f}\) (módulo de punto flotante) Calcula el resto de la división de dos números de punto flotante.. Si el valor del acimut es negativo, \(360\) Se añaden grados para hacerlo positivo.:
\(\texto{azimut} = \begin{casos}
\texto{azimut} + 360.0 & \texto{si } \texto{azimut} < 0.0 \\
\texto{azimut} & \texto{de lo contrario}
\final{casos}\)Inversión de la dirección de rotación
Luego se invierte el acimut ajustado para realizar la rotación en la dirección opuesta.:
\(\texto{azimut} = -\text{azimut}\)
Conversión de grados a radianes
El acimut en grados se convierte a radianes., Como las funciones trigonométricas utilizan radianes:
\(\texto{radianes} = \frac{\texto{azimut} \times \pi}{180.0}\)
Cálculo de nuevas coordenadas
El nuevo \(x\) y \(y\) Las coordenadas se calculan aplicando la rotación en el \(XY) plano alrededor de un origen \((x_0, y_0)\). Las fórmulas utilizadas son:
\(
p_x = \left( (X - x_0) \por cos(\texto{radianes}) + (y - y_0) \veces sin(\texto{radianes}) \bien) + x_0)\(
p_y = \left( -(X - x_0) \veces sin(\texto{radianes}) + (y - y_0) \por cos(\texto{radianes}) \bien) + y_0\)Dónde \((X, y)\) son las coordenadas iniciales del punto, y \((x_0, y_0)\) son las coordenadas del origen.
Conservación de la coordenada Z
Él \(z\) La coordenada del punto original permanece inalterada durante la rotación.:
\(y_{\texto{final}} =z_{\texto{inicial}}\)
Resultado final
El resultado del procedimiento es un nuevo punto con coordenadas \((p_x, p_y, z)\), donde \(p_x\) y \(p_y\) son las nuevas coordenadas en el \(XY) avión después de la rotación, y \(z\) es la coordenada original en el \(Z) eje.
\(\texto{Nuevo punto} = \{ p_x, p_y, z \}\)
