Validación de la teoría
Reflejos
Validar la teoría detrás de cualquier herramienta de optimización es esencial para garantizar su aplicabilidad en operaciones mineras del mundo real.. Esta página aclara cómo se verifican los fundamentos matemáticos de MiningMath y qué significa eso para la confiabilidad de la planificación..
- Demuestra cómo el motor de optimización de MiningMath se adhiere a las formulaciones académicas, garantizar la coherencia con los marcos teóricos conocidos.
- Ofrece transparencia a través de modelos y scripts replicables, Permitir a los profesionales probar escenarios frente a los comportamientos esperados.
- Respalda la confianza en los resultados al alinear la lógica de implementación con estándares matemáticos probados, Reducir el riesgo en la toma de decisiones prácticas.
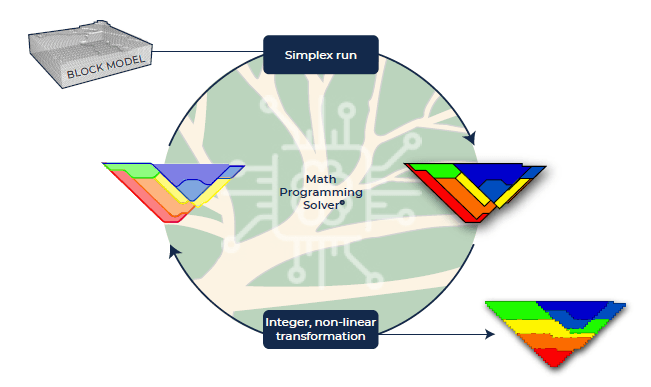
Los resultados de MiningMath solo son posibles gracias a su Solucionador de Programación Matemática patentado ©. Consiste en una Programación Lineal Entera Mixta (MILP) formulación y métodos de linealización que abordan los desafiantes aspectos no lineales de la optimización minera. Además, tiene su propia sucursal & Cut, que proporciona más eficiencia que los optimizadores MILP estándar, ya que está ajustado a este problema de optimización específico.
Otra gran ventaja de MiningMath proviene de las formulaciones matemáticas basadas en superficies. (Goodwin et al., 2006; Mariño, 2013), en lugar de las precedencias de bloque habituales. Los métodos de precedencia de bloques pueden conducir a mayores errores (Beretta y Marinho, 2014), proporcionando pendientes más empinadas (es decir. más arriesgado, más optimista) de lo solicitado. El uso de superficies elimina estos errores geotécnicos y permite zonas geotécnicas bloque por bloque., si es necesario.
Estas formulaciones basadas en superficies permiten que MiningMath incluya restricciones geométricas, y, como consecuencia, encontrar soluciones más cercanas a las operaciones mineras reales. El usuario puede guiar geometrías incluyendo minería y anchos de fondo, longitudes de minería, tasas máximas de avance vertical, y forzar/restringir áreas mineras. Puede comprender mejor cómo interactúa cada restricción con todas las demás aquí. Tales restricciones dan libertad al usuario para trabajar, O no, con cortes y retrocesos predefinidos que podrían limitar el espacio de posibles soluciones. También se puede ver una vista en profundidad de las formulaciones y el algoritmo de MiningMath. aquí.
Este enfoque (Figura 1) ha sido aplicado durante años por los clientes, como vale, Río Tinto, Codelco, Kinross, AMSA y MMG, con un número creciente de licencias vendidas, Comunicados de prensa y investigación académica demostrando también la consistencia de la implementación. Con desarrollos constantes desde 2013, MiningMath ha alcanzado un estado maduro y robusto. Es el primer y único motor de optimización de minería de un solo paso disponible en el mercado..
Figura 1: El enfoque de MiningMath. Desde el modelo de bloques hasta el cronograma en un solo paso resuelto por su exclusivo Solucionador de Programación Matemática ©.