Algoritmo de optimización de minería

Lectura estimada: 15 minutos 3062 puntos de vista

MiningMath tiene un algoritmo de optimización de minería flexible que consiste en un Programación lineal entera mixta (MILP) formulación y métodos de linealización que abordan los desafiantes aspectos no lineales del problema. Además, MiningMath tiene su propia Sucursal & Algoritmo de corte, que proporciona más eficiencia que los optimizadores MILP estándar, ya que está ajustado a este problema de optimización específico.

Una de las principales ventajas de MiningMath proviene de las formulaciones matemáticas basadas en superficies [1] [2] , en lugar de las precedencias de bloque habituales. Los métodos de precedencia de bloques pueden conducir a mayores errores [3] , proporcionando pendientes más empinadas (es decir. más arriesgado, más optimista) de lo solicitado. El uso de superficies elimina estos errores geotécnicos y permite zonas geotécnicas bloque por bloque, si es necesario.

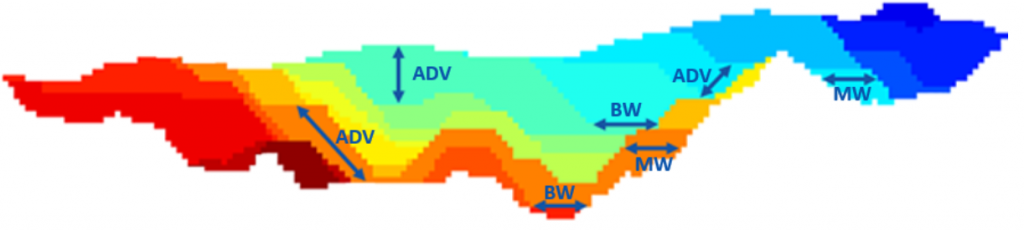
Otra ventaja crucial es que la formulación de MiningMath incluye restricciones geométricas, permitiendo que su algoritmo encuentre soluciones que sean más cerca de las operaciones mineras reales. El usuario puede geometrías de guía al incluir anchos de minería y de fondo, tasas máximas de avance vertical, y forzar/restringir áreas mineras. Tales restricciones dan libertad al usuario para trabajar, O no, con cortes y retrocesos predefinidos que podría limitar el espacio de posibles soluciones. Por eso, el software proporciona diferentes vistas y soluciones para la misma mina para cada parámetro cambiado.

Finalmente, las soluciones lineales deben asignarse a un número entero aproximado (bloque por bloque) solución que representará la programación del problema minero en el mundo real. Él inteligencia para convertir soluciones continuas en enteros y los no lineales son hechos por la sucursal de MiningMath & Algoritmo de corte.

Diagrama de flujo del algoritmo y formulación matemática.

MiningMath emplea una formulación matemática innovadora y una potente propiedad Branch & Algoritmo de corte para problemas de optimización de minería. A continuación se proporciona una descripción de esta formulación matemática y los tres pasos principales del algoritmo empleado..

Paso 1: Evaluación inicial

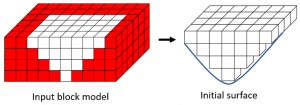
Figura 1: Evaluación inicial del modelo de bloque completo e inclusión de bloques rentables probables dentro de una superficie inicial.

El primer paso del algoritmo de optimización de minería es eliminar regiones que no agregan ningún valor al proyecto. Esta es una evaluación inicial que considera las limitaciones de la pendiente., reduciendo el tamaño del problema y proporcionando una región de interés para el proceso de optimización. Dado que MiningMath siempre emplea superficies en sus formulaciones matemáticas, este primer conjunto de bloques rentables probables están contenidos dentro de una superficie inicial como se muestra en la Figura 1.

Paso 2: Linealización de problemas y optimización de minería

En el segundo paso del algoritmo de optimización de minería, el no lineal, problema de números enteros se aproxima a un número entero, lineal basado en superficies. Para eso, primero es necesario definir la notación común a través del problema y sus variables.

\(S\): número de modelos de yacimientos simulados considerados
\(s\): índice de simulación, \(s = 1,...,S \)
\(D\): número de destinos
\(d\): índice de destino, \(d = 1,...,D \)
\(Z\): número de niveles en el modelo de yacimiento
\(z\): índice de nivel, \( z = 1,...,Z \)
\(T\): número de períodos durante los cuales se programa el yacimiento y también define el número de superficies consideradas
\(t\): índice de período, \(t = 1,...,T. \)
\(M\): número de células en cada superficie; donde \(M = x \times y\) representa el número de bloques mineros en dimensiones x e y.
\(c\): índice de celda, \(c = 1, \ldots ,M\).
\(G\): número de grupos de destino únicos definidos. Cada grupo puede contener 1, todos, o cualquier combinación de destinos.
\(g\): índice de grupo, \(g = 1, \ldots ,G\).

\(x_{c,t,d}^{z}\): variable binaria independiente de la simulación que asume 1 si bloque \((c, z)\) se está extrayendo en el período \(t\) y enviado a destino \(d\), y 0 de lo contrario.
\(e_{c,t}\): variables continuas independientes de la simulación asociadas con cada celda \(c\) para cada período \(t\), representando elevaciones de celdas.
\(\overline{f_{t,g,s}},\underline{f_{t,g,s}}\): variables continuas para penalizar las restricciones de suma violadas para cada período, grupo de destinos, y simulación. Es necesario un par de variables para cada parámetro cuantificable modelado bloque por bloque cuya suma se está restringiendo. Un ejemplo serían las variables utilizadas para controlar las horas de flota gastadas en diferentes períodos, grupos de destinos, y simulaciones. Más información sobre posibles parámetros aquí. Tenga en cuenta también que el software permite el control de la media de las simulaciones, en lugar de tratar con cada simulación individualmente, y el control por la suma de destinos, en lugar de cada destino individualmente.
\(\overline{\alpha_{t,g}},\underline{\alpha_{t,g}}\): pesos definidos por el usuario para las variables \(\overline{f_{t,g,s}},\underline{f_{t,g,s}}\) con el mismo grupo de destino \(g\) y periodo \(t\). Estos sólo se pueden definir en el .ssscn archivos.
\(\overline{j_{t,g,s}},\underline{j_{t,g,s}}\): variables continuas para penalizar las restricciones promedio violadas para cada período, destino, y simulación. Se necesita un par de variables para cada parámetro cuantificable modelado bloque por bloque cuyo promedio se está restringiendo. Un ejemplo serían las variables utilizadas para controlar la ley promedio de los bloques extraídos en diferentes períodos., grupos de destino, y simulaciones. Más información sobre posibles parámetros aquí. Tenga en cuenta también que el software permite el control de la media de las simulaciones, en lugar de tratar con cada simulación individualmente, y el control por la suma de destinos, en lugar de cada destino individualmente.
\(\overline{\beta_{t,g}},\underline{\beta_{t,g}}\): pesos definidos por el usuario para las variables \(\overline{j_{t,g,s}},\underline{j_{t,g,s}}\) con el mismo destino \(d\) y periodo \(t\). Estos sólo se pueden definir en el .ssscn archivos.

\(e_{c,t} \in \mathbb{R},\,\, \) \(t = 1,...,T\),\(c=1,...,M\)
\(x_{c,t,d}^{z} \in \{0,1\},\,\, \) \(c=1,...,M\), \(t = 1,...,T\), \(z=1,...,Z\), \(d=1,...,D\)
\(\overline{f_{t,d,s}},\underline{f_{t,d,s}} \in \mathbb{R_{\geq 0}}\), \(t = 1,...,T\), \(s=1,...,S\), \(d=1,...,D\)
\(\overline{j_{t,d,s}},\underline{j_{t,d,s}} \in \mathbb{R_{\geq 0}}\), \(t = 1,...,T\), \(s=1,...,S\), \(d=1,...,D\)

Tener definido el conjunto de variables, ahora es posible definir un modelo matemático con una función objetivo y las restricciones necesarias.

Función objetiva
idea intuitiva
Suma del valor económico de los bloques extraídos por período, destino, y simulación.
Promedie el resultado por el número de simulaciones.
Reste las penalizaciones por ciertas restricciones violadas asociadas con algunos parámetros definidos por el usuario.
Requisitos
\(V_{c,t,d,s}^{z}\): valor económico acumulado descontado del bloque \((c, z)\) en simulación \(s\), período \(t\) y destino \(d\). Más sobre este cálculo aquí.
Formulación
\(max\frac{1}{s}\)\(\sum\limits_{s=1}^{S}\sum\limits_{t=1}^{T}\sum\limits_{c=1}^{M}\sum\limits_{z=1}^{Z}\sum\limits_{d=1}^{D}\)\((V_{c,t,d,s}^{z} x_{c,t,d}^{z}) \,-\, p\)
donde
\(p = \sum\limits_{t=1}^{T}\sum\limits_{g=1}^{G}(\overline{\alpha_{t,g}}(\sum\limits_{s=1}^{S}\overline{f_{t,g,s}})\)\( + \underline{\alpha_{t,g}}(\sum\limits_{s=1}^{S}\underline{f_{t,g,s}})\)\( + \superposición{\beta_{t,gramo}}(\suma límites_{s = 1}^{S}\superposición{j_{t,gramo,s}})\)\( + \underline{\beta_{t,g}}(\sum\limits_{s=1}^{S}\underline{j_{t,g,s}})) \)

Finalmente, la función objetivo está restringida por las siguientes restricciones

\(mi_{C,t-1} - mi_{C,t} \edad 0, c=1,...,M, t=2,...,T \)

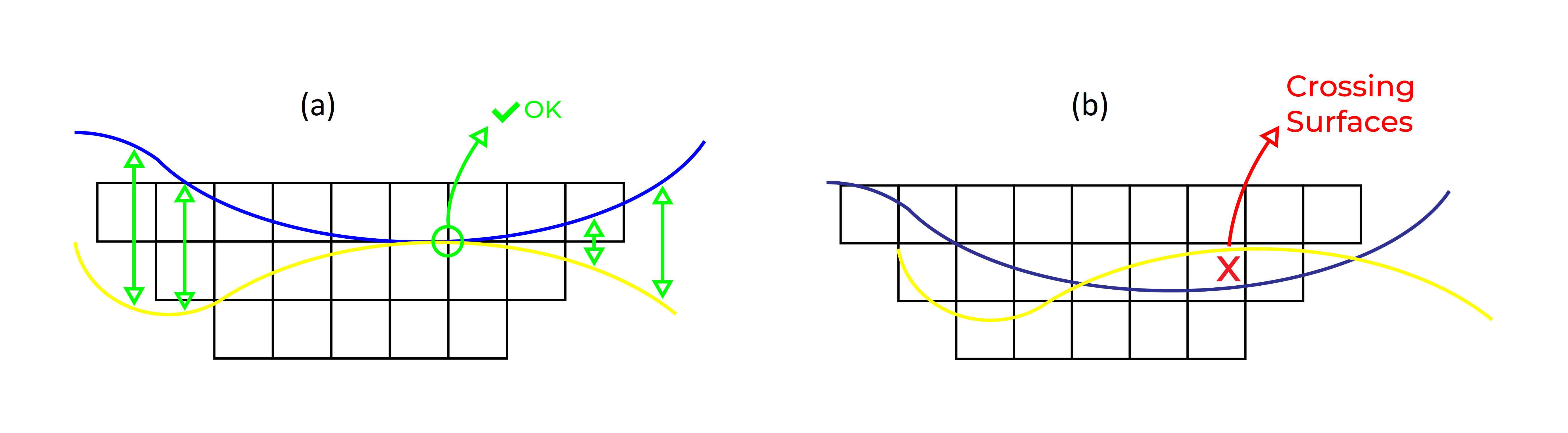
Figura 3: Ejemplo de cruce de superficies — Figura 3: dos superficies (azul y amarillo): a) no cruzarse entre sí y respetar la restricción (2); B) cruzarse entre sí y no respetar la restricción (2).

idea intuitiva

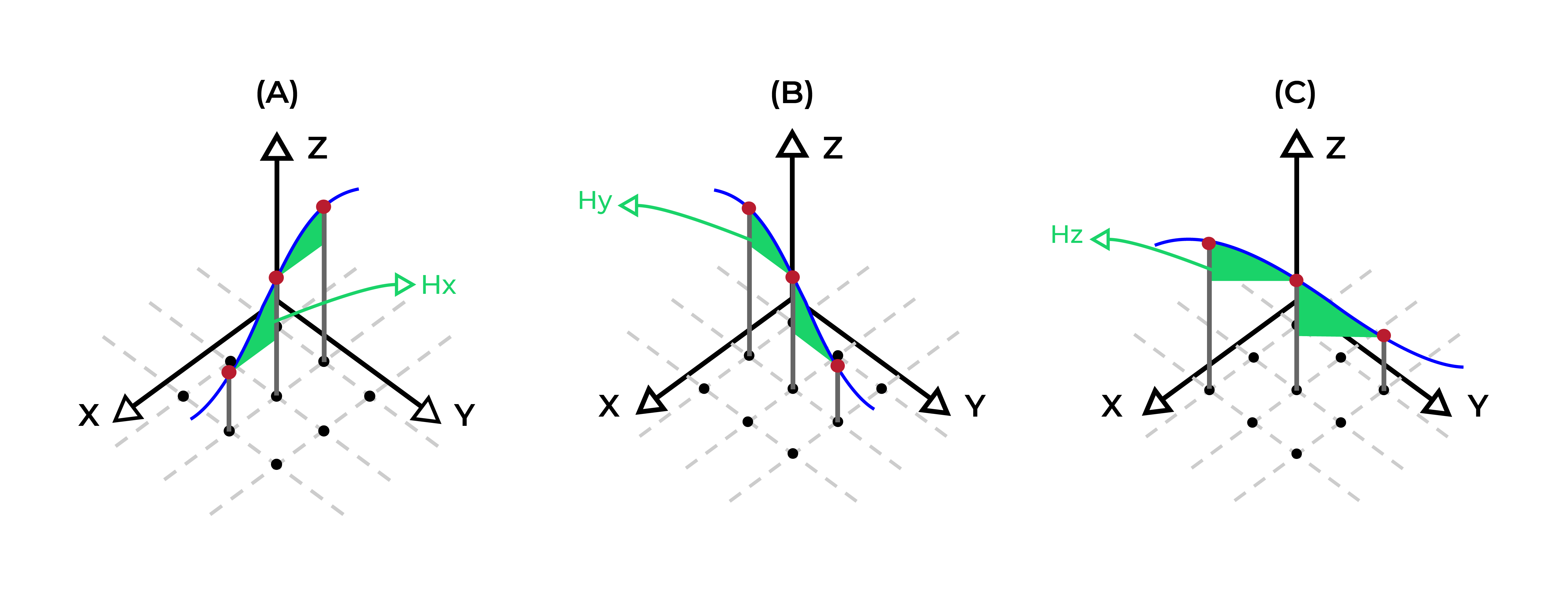
Las elevaciones adyacentes en una sola superficie deben respetar una diferencia máxima. Este máximo cambiará según la dirección en la que estén adyacentes.: X, y, o en diagonal.

Requisitos

\(H_x, hola, H_d\): diferencia máxima en elevación para celdas adyacentes en \(x\), \(y\) y direcciones diagonales
\(X_c, Y_c, D_c\): equivalente a \(H_x, hola, H_d\)concepto, los conjuntos de celdas adyacentes, lateralmente en \(x\), en \(y\), y en diagonal, para una celda dada \(c\), respectivamente.

Formulación

\(mi_{C,t} - mi_{X,t} \ge H_x, c=1,...,M, t=1,...,T, x \in X_c\)
\(mi_{C,t} - mi_{y,t} \ge H_y, c=1,...,M, t=1,...,T, y \in Y_c \)
\(mi_{C,t} - mi_{d,t} \ge H_d, c=1,...,M, t=1,...,T, d \in D_c \)

Ejemplo de restricciones de pendiente en el algoritmo de optimización de minería — Figura 4: Diferencia máxima permitida (Hx, hola, y alta definición) en elevación entre celdas adyacentes en contacto lateralmente en la dirección x (a), en contacto lateralmente en la dirección y (B), y en contacto en diagonal (C).

Restricciones de propiedad no reveladas. Posibles ejemplos de restricciones del mismo tipo, pero no los realmente empleados.

idea intuitiva

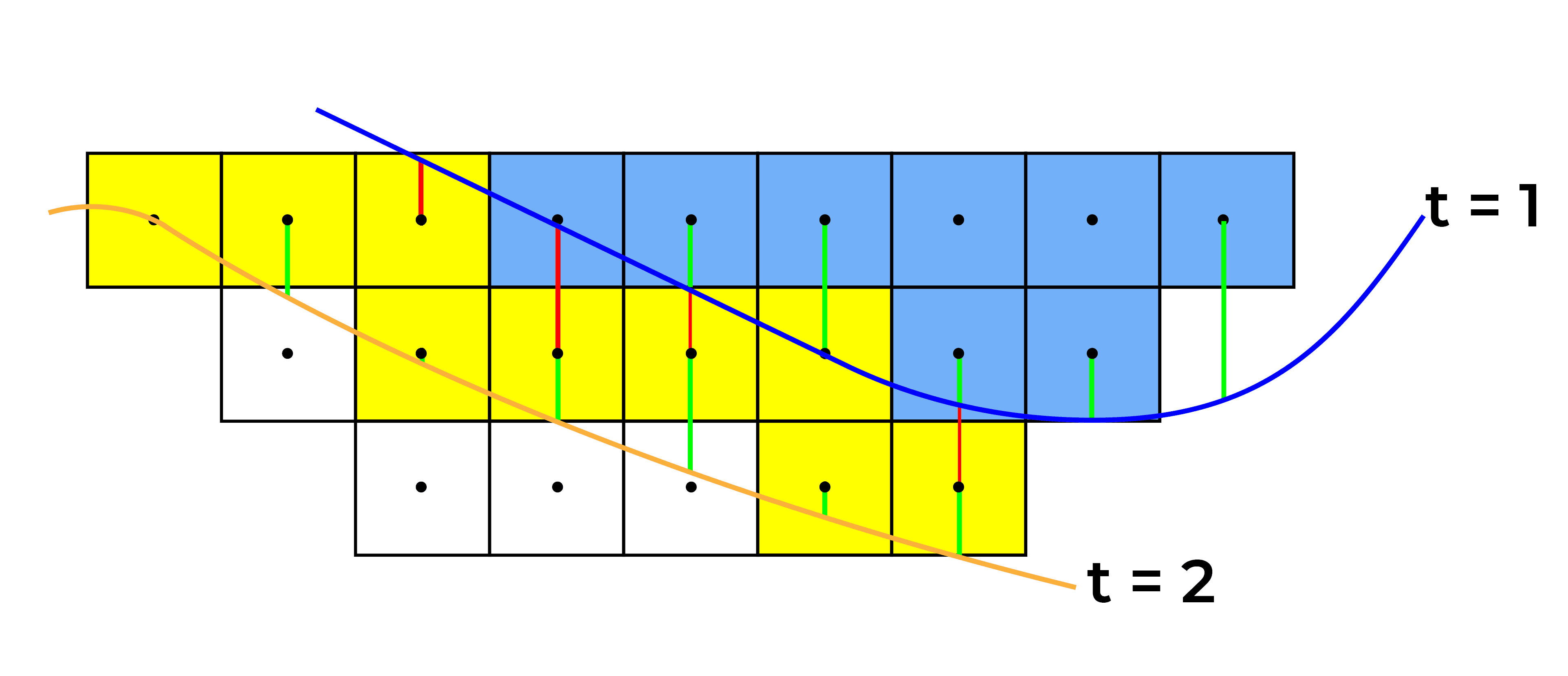
Las superficies definirán cuándo se extraerán los bloques. Por ejemplo, bloques entre superficies asociadas con el período 1 y 2, se extraerá en el período dos. Un bloque está entre dos superficies si su centroide está entre las dos superficies.

Requisitos

\(MI_{C}^{z}\): elevación del centroide para un bloque dado \((C, z)\)

Formulación

\(MI_{C}^{z} \veces sumalímites_{re=1}^{D}X_{C,1,d}^{z} \ge e_{C,1}, c=1,...,M, z=1,...,Z)
\(mi_{C,t-1} \ge E_{C}^{z} \veces sumalímites_{re=1}^{D}X_{C,t,d}^{z} \ge e_{C,t}, \)\(c=1,...,M, t=2,...,T, z=1,...,Z)

Figura 5: Distancia entre centroides sobre superficies (lineas verdes) y debajo de las superficies (líneas rojas) respetando las restricciones (6) y (7). Los bloques azules se extraen en el período 1, mientras que los bloques amarillos se extraen en el período 2.

idea intuitiva

Cada bloque minado solo se puede enviar a un destino.

Formulación

\(\suma límites_{re = 1}^{D}X_{C,t,d}^{z} = 1, c=1,....,M, t=1,...,T, z = 1,...,Z\)

idea intuitiva

Para cada período y grupos de destino existe un límite superior e inferior de tonelaje total a extraer. Los grupos de destinos pueden estar formados por cualquier combinación única de destinos, con 1, muchos o todos. La suma del tonelaje de bloques minados enviados a un mismo grupo de destinos en el mismo período debe respetar estos límites.

Requisitos

\(T_c^z): tonelaje para un bloque dado \((C, z)\).
\(\superposición{T_{t,gramo}}\): límites superiores en el tonelaje total a extraer durante el período \(t\) y destinos en grupo \(g\).

Formulación

\( \suma límites_{c=1}^M\sum\limits_{z=1}^{Z}\suma límites_{d \in g}T_c^z x_{C,t,d}^{z} \dejar_{t,gramo}, t = 1,...,T, gramo = 1,..., G\)

idea intuitiva

El usuario puede definir un determinado parámetro. (es decir. horas de flota dedicadas) asociado con cada bloque minado para tener su suma controlada. La suma de los valores de este parámetro asociado a cada bloque minado debe respetar cotas inferior y superior para cada periodo, grupos de destino (opcional) y simulación (individualmente o en promedio). Los grupos de destinos pueden estar formados por cualquier combinación única de destinos, con 1, muchos o todos.

Requisitos

\(\subrayar{F_{t,gramo,s}},\superposición{F_{t,gramo,s}}\): límites inferior y superior, respectivamente, en suma del parámetro definido por el usuario a respetar en el período \(t\), grupo de destino \(g\), y simulación \(s\).
\(F_{C,d,s}^{z}\): valor del parámetro definido por el usuario relacionado con un bloque dado \((C, z)\) en destino \(d\) y simulación \(s\).

Formulación

\(\subrayar{F_{t,gramo,s}} \le \sum\limits_{c=1}^M\sum\limits_{z=1}^{Z}\suma límites_{d \in g}F_{C,d,s}^{z}X_{C,t,d}^{z} + \subrayar{F_{t,gramo,s}} - \superposición{F_{t,gramo,s}} \le \overline{F_{t,gramo,s}},\)
\(t = 1,...,T, gramo = 1,..., GRAMO, s = 1,..., S\)

idea intuitiva

El usuario puede definir un determinado parámetro. (es decir. calificación) asociado a cada bloque minado a controlar en promedio. este promedio es ponderado por el tonelaje del bloque y por un opcional, peso definido por el usuario. Debe respetar límites inferior y superior para cada período., grupo de destino (opcional) y simulación (individualmente o en promedio). Los grupos de destinos pueden estar formados por cualquier combinación única de destinos, con 1, muchos o todos.

Requisitos

\(\subrayar{J_{t,gramo,s}},\superposición{J_{t,gramo,s}}\): límites inferior y superior, respectivamente, para que se respete el valor promedio del parámetro definido por el usuario en el período \(t\), simulación \(s\), y grupo de destino \(g\).
\(T_{C}^{z}\): tonelaje para un bloque dado \((C, z)\).
\(J_{C,s,d}^{z}\): valor del parámetro definido por el usuario del bloque \((C, z)\) enviado a destino \(d\) en simulación \(s\)
\(PAGS_{C,t,d,s}^{z}\): peso definido por el usuario para el bloque \((C, z)\) en período \(t\), destino \(d\), y simulación \(s\)

Formulación

\(\subrayar{J_{t,gramo,s}} \le\)\(\fractura{\suma límites_{c=1}^M\sum\limits_{z=1}^Z\sum\limits_{d\in g}PAGS_{C,t,d,s}^{z}T_{C}^{z}J_{C,s,d}^{z}X_{C,t,d}^{z}}{\suma límites_{c=1}^M\sum\limits_{z=1}^Z\sum\limits_{d\in g}PAGS_{C,t,d,s}^{z}T_{C}^{z}}\)\( + \subrayar{j_{t,gramo,s}} - \superposición{j_{t,gramo,s}} \le \overline{J_{t,gramo,s}}\)
\(t = 1,...,T, gramo = 1,..., GRAMO, s = 1,..., S\)

Restricciones de propiedad no reveladas

idea intuitiva

Las superficies deben respetar los parámetros geométricos definidos por el usuario, como el ancho inferior mínimo, ancho mínimo de minería, longitud mínima de minado, y velocidad vertical máxima de avance, como se representa aquí.

Formulación

\(Geométrico(mi_{C,t}) \archivo text{restricción geométrica}, c=1,...,M, t=1,...,T)

Paso 3: Entero, solución no lineal y evaluación

El siguiente paso en el algoritmo de optimización de minería es convertir la solución lineal a un número entero, uno no lineal. Rama de MiningMath & método de corte es responsable de esta conversión. Una vez hecho, la solución resultante se puede evaluar, que lleva al final de la ejecución del algoritmo o a un nuevo proceso de optimización. este nuevo el proceso podría desencadenarse si se presenta una de las dos situaciones:

se violan las restricciones debido a la transformación de lineal a entero, solución no lineal, o debido a que el problema es inviable.
una evaluación de ciertas restricciones en el entero transformado, solución no lineal concluyó que podrían no afectar el problema y ser mejor desechados o modificados.

Si alguno de estos es cierto, la solución en esta etapa se enviará de vuelta al Paso 2 para linealización y refinamiento. Por lo tanto, si este refinamiento es causado por la situación 1) entonces el objetivo es mejorar la viabilidad de la solución. Esta viabilidad se mejora de acuerdo con el orden de la jerarquía de restricciones que se muestra en la Figura 6.

Figura 6: Corden de jerarquía de restricciones.

A diferencia de, si es causado por la situación 2) entonces el objetivo es permitir que la optimización se centre en los cuellos de botella del problema y mejore el VAN actual. Una vez que no se ha identificado ninguna de estas situaciones, se devuelve la solución actual. Tenga en cuenta que cada vez que el algoritmo vuelve al paso 2, se realiza una nueva optimización global, por lo tanto, la nueva solución resultante podría ser completamente diferente.

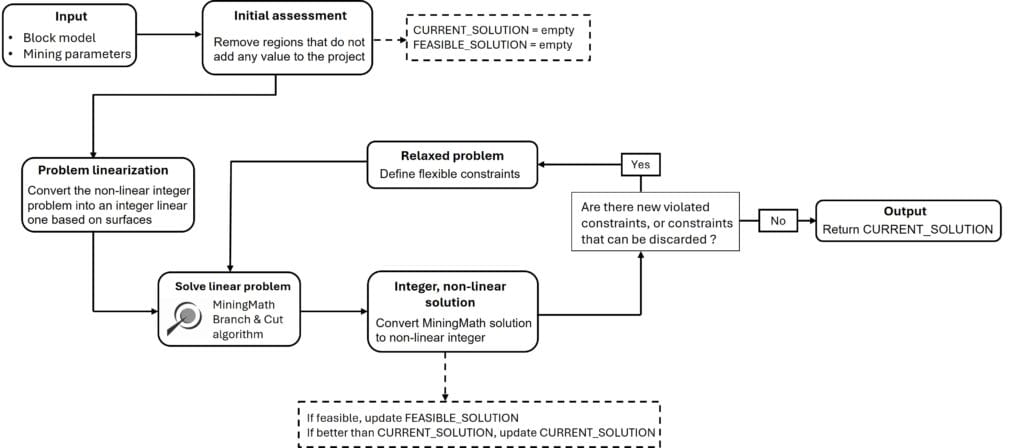
pseudo-código

Todo el proceso del algoritmo de optimización de minería., de entrada a salida se resume en el pseudo-código a continuación. Se hacen referencias a pasos anteriores 1, 2, y 3. Este flujo algorítmico, junto con la formulación matemática propuesta, ejemplifica la metodología innovadora aplicada para resolver un problema de programación de una sola mina..

				
					INPUT: Block model,
       Mining parameters,
       Optional time limit T
OUTPUT: Excel report summarizing the main results of the optimization,
        Outputs of mining optimization, topography, and pit surfaces using   
        .csv format that can also be imported into other mining packages.

EXECUTE initial assessment // Step 1
CREATE problem linearization P // Step 2
SET CURRENT_SOLUTION to empty
SET FEASIBLE_SOLUTION to empty
REPEAT // Step 3
    SOLVE P // Optimization engine + proprietary Branch & Cut algorithm
    SET LS to the integer, linear solution of P
    TRANSFORM LS to an integer, non-linear solution RS
    
    // Evaluate RS
    IF RS has no violated constraints THEN
        SET FEASIBLE_SOLUTION to RS
    ENDIF
        
    IF RS is better than CURRENT_SOLUTION THEN 
        SET CURRENT_SOLUTION to RS
    ENDIF
    
    // Evaluate if new iteration is necessary
    IF FEASIBLE_SOLUTION is empty THEN
        // Step 2 and Figure 6
        CREATE new problem linearization P
               with flexible constraints
        CONTINUE // Go back to loop's start
    ELSE IF T has been reached
        BREAK // Leave loop
    ELSE IF RS has violated constraints that were unviolated in LS OR
          has constraints that can be discarded/modified THEN
        CREATE new problem linearization P // Step 2
        CONTINUE // Go back to loop's start
    ELSE
        BREAK // Leave loop
    ENDIF
WHILE TRUE
EXPORT reports and outputs from CURRENT_SOLUTION

MiningMath

Loading...

Algoritmo de optimización de minería

Diagrama de flujo del algoritmo y formulación matemática.

Paso 1: Evaluación inicial

Paso 2: Linealización de problemas y optimización de minería

Función objetiva

Paso 3: Entero, solución no lineal y evaluación

pseudo-código

CONTENIDO

MiningMath

Loading...

Algoritmo de optimización de minería

Diagrama de flujo del algoritmo y formulación matemática.

Paso 1: Evaluación inicial

Paso 2: Linealización de problemas y optimización de minería

Función objetiva

Restricciones de superficie

Restricciones de pendiente

Restricciones de enlace

Restricciones de destino

Restricciones mineras

Restricciones de suma

Restricciones promedio

Restricciones geométricas

Paso 3: Entero, solución no lineal y evaluación

pseudo-código

Algoritmo de optimización de minería

CONTENIDO