Validación de superficies
Reflejos
Validating surface integrity is essential to ensure that mine plans align with design constraints and field data, reducing rework and improving confidence in operational decisions.
- Reliable model alignment: MiningMath compares surfaces numerically and visually with reference topographies, enabling early validation as part of its integrated single-step optimization.
- Error prevention in geometry: Deviations are flagged before execution, avoiding downstream issues. Surface checks are embedded alongside constraint tuning.
- Credibility for decision-making: Based on peer-reviewed methods and global use, MiningMath’s validation supports internal approval processes and scripted scenario testing via API.
El mejor forma generar superficies es mediante el uso de una superficie topográfica creada por MiningMath, que se crea después de la Validación de datos, después manipulando solo las coordenadas Z. Asegurate que cumplir con todos los requisitos de superficie revelado aquí.
Encabezados debe ser nombrado como X, Y, y Z. Estos archivos tienen que obedecer un orden de valor ascendente en cada uno de los ejes.
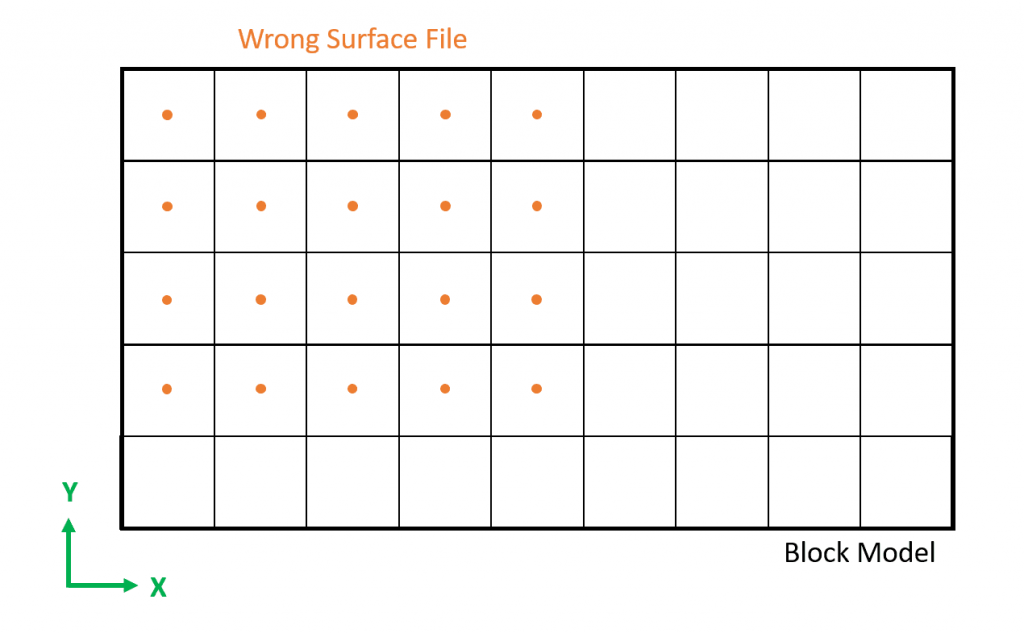
Mismo tamaño del modelo de bloque., artículo 1.1 de esta pagina lo explica.
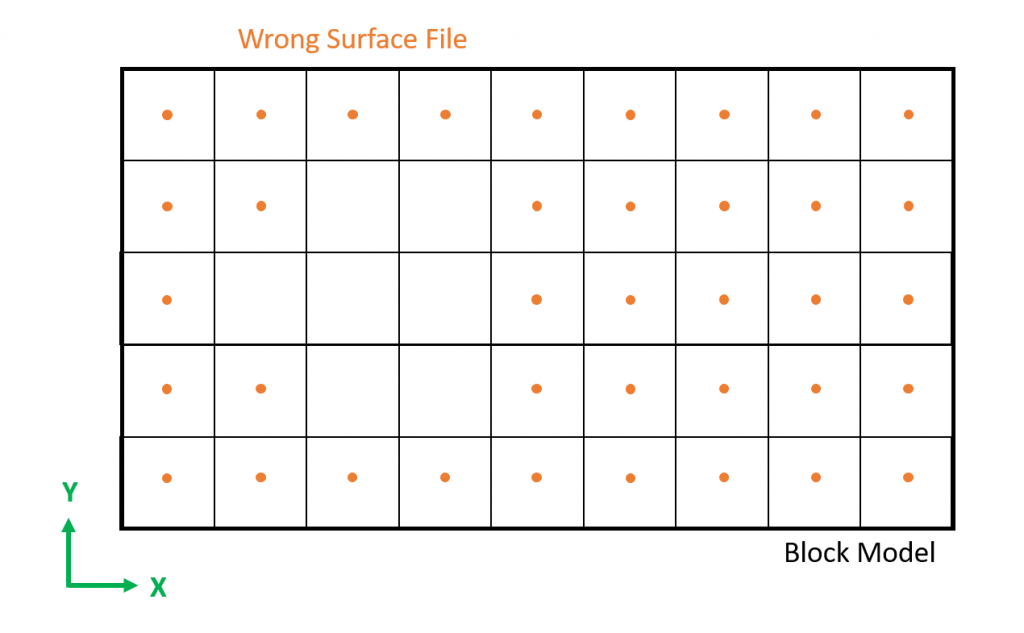
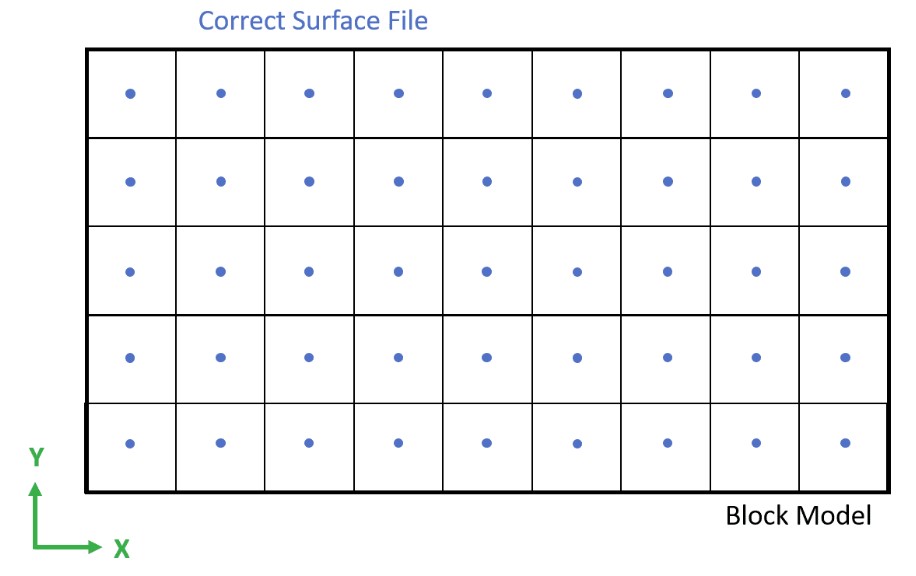
Es los puntos deben estar alineados con los centroides de los bloques, elementos 1.1 y 1.2 te ayudo a entenderlo.
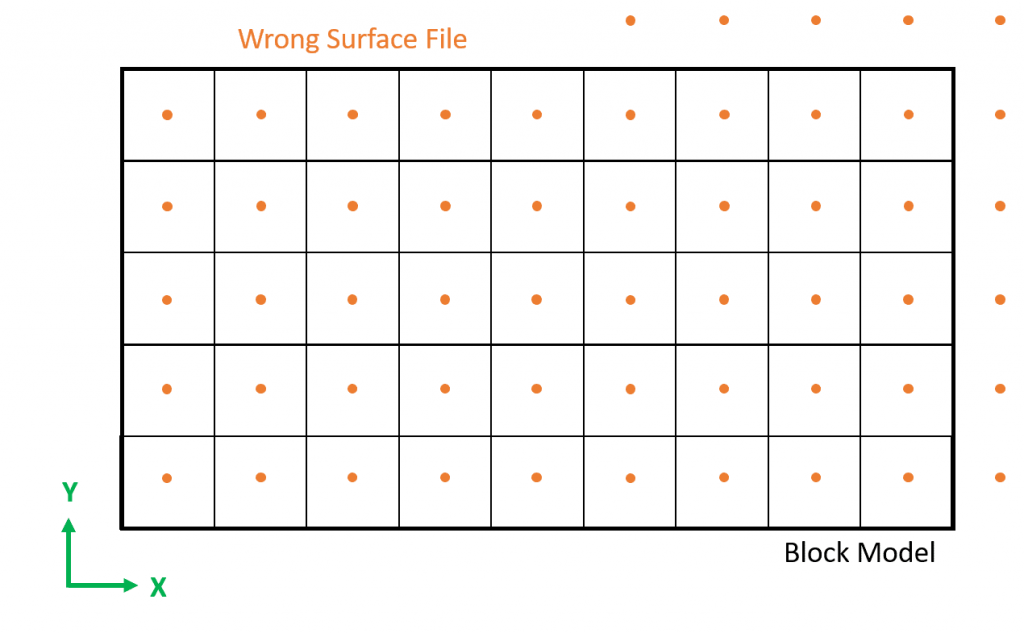
Definido como un grilla de puntos, la validación visual, artículo 1.2 lo muestra.
estar en el formato CSV.
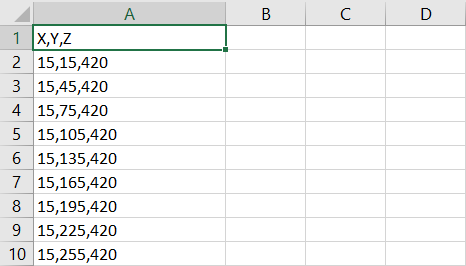
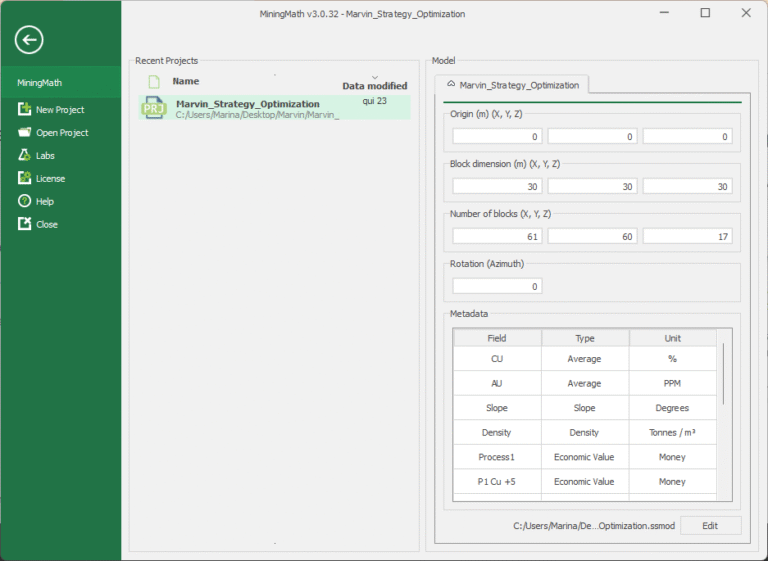
Mediante el uso de los valores de un archivo de depósito de Marvin en Figura 2, encontramos el modelo de bloque límites de los centroides que comienzan en Xmín=15; YMin=15 y tiene el valor centroide máximo de Xmáx=5295; Ymáx=8,265, lo cual se pudo confirmar revisando la topografía generada por MiningMath.
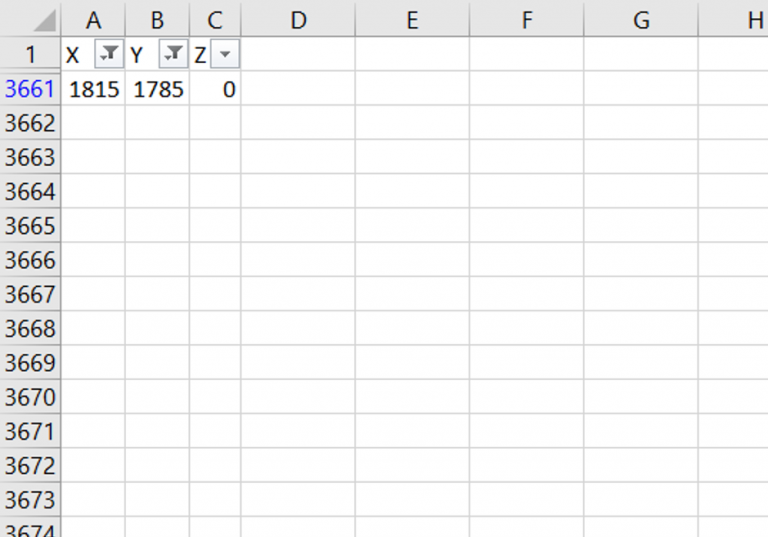
Entonces, es tiempo de buscar tus limites superficiales, en este ejemplo el archivo elegido fue “Superficie-RM-offset-300m”. La manera fácil de encontrarlo, es filtrando los valores del eje, como se muestra en Figura 3, que reveló Xmín= 15; YMín=15 y Xmáx= 1,815 y Ymáx= 1,785. Por lo tanto, a pesar de que este archivo también se basó en Marvin Deposit, no es posible usarlo ya que la superficie es más pequeña que el modelo de bloques en su lugar, lo que significa que no tiene el mismo tamaño que el archivo del modelo de bloques.
Siempre vale la pena comprobar los límites de la superficie diseñada (Cifras 4 para 8) si nos enfrentamos a un error. Recuerda eso todo, incluso elevaciones, debe estar en los límites del modelo de bloques y consulta las recomendaciones para tu superficie.
Él centroides límite máximo usando la ecuación para cada eje:
Valor centroide máximo = OX + (NX*DX)-(DX/2)
Dónde:
OX es el origen del eje X;
DX es la dimensión de bloque del eje X;
NX es el número de bloques en el eje X.
Nota: (DX/2) está relacionado con la distancia que se debe sumar en el origen para encontrar el centroide del primer bloque, o reducido en el límite del modelo de bloques para encontrar el último centroide, ya que los orígenes se basan en la esquina del modelo de bloque.
El siguiente video presenta cómo validar superficies numérica y visualmente. Esta verificación inicial es la que te permite entender qué puede estar pasando y dónde está el error.. El ejemplo utilizado con respecto al mensaje.: “Error al analizar la superficie: Las coordenadas no están espaciadas correctamente” pero se adapta a cualquier caso en el que las superficies utilizadas causen un problema, especialmente cuando un error de caja roja aparece.
En este caso, ya que hay muchos valores que no coinciden con los correctos para X e Y, la manera más rápida y fácil para arreglarlo es reiniciar desde el principio.
Video 1: Validación de superficies.
Problemas comunes
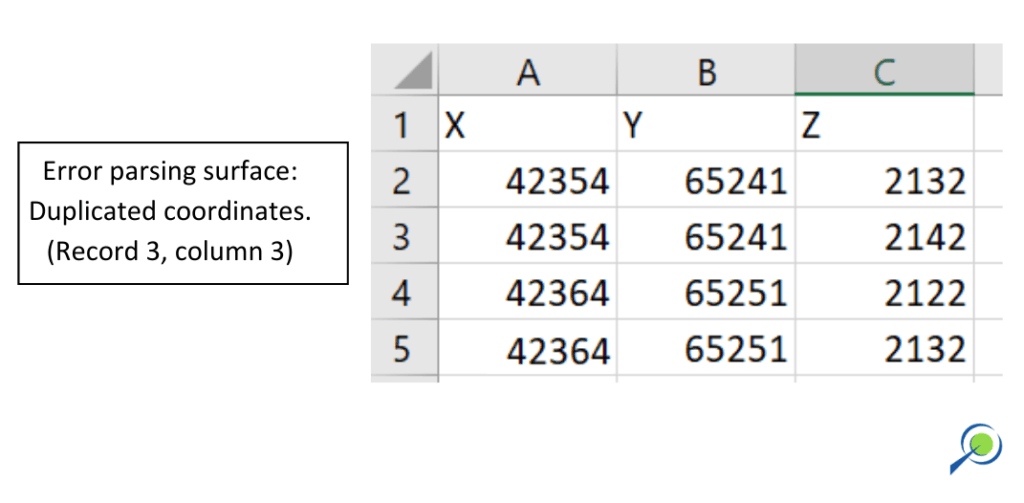
- Error al analizar la superficie: coordenada duplicada
Si aparece este mensaje, Es posible que su archivo de superficie contenga más de una elevación para la misma coordenada. Por favor revise el archivo CSV.
