Sugerencias de optimización
Destacados
Las operaciones mineras se benefician cuando la optimización no está sobrecargada con restricciones. Este enfoque ayuda a exponer el verdadero potencial económico de la mina..
- Comenzar con restricciones mínimas permite a MiningMath buscar ampliamente y encontrar mejores programaciones, reduciendo iteraciones y reelaboraciones manuales.
- Agregar restricciones gradualmente permite a MiningMath evaluar el costo de cada una., Ayudar a los equipos a alinear los límites operativos con la rentabilidad.
- Pequeños cambios en parámetros como la capacidad del molino o la tasa de descuento ayudan a MiningMath a escapar de las trampas locales y revelar estrategias de mayor valor..
Impacto de las restricciones en la optimización del VPN
La relación entre el número de restricciones y el Valor Actual Neto (VAN) es generalmente inversamente proporcional. Los escenarios con menos restricciones permiten que el algoritmo de optimización busque con mayor libertad, A menudo conduce a resultados de VPN más altos. Por lo tanto, se recomienda explorar primero todo el potencial de un proyecto minero., Empezando con el Validación de datos procedimiento, Seguido de los otros posibles Flujos de trabajo que puedan servir de base para los pasos siguientes.
Un estudio sobre los impactos de las restricciones
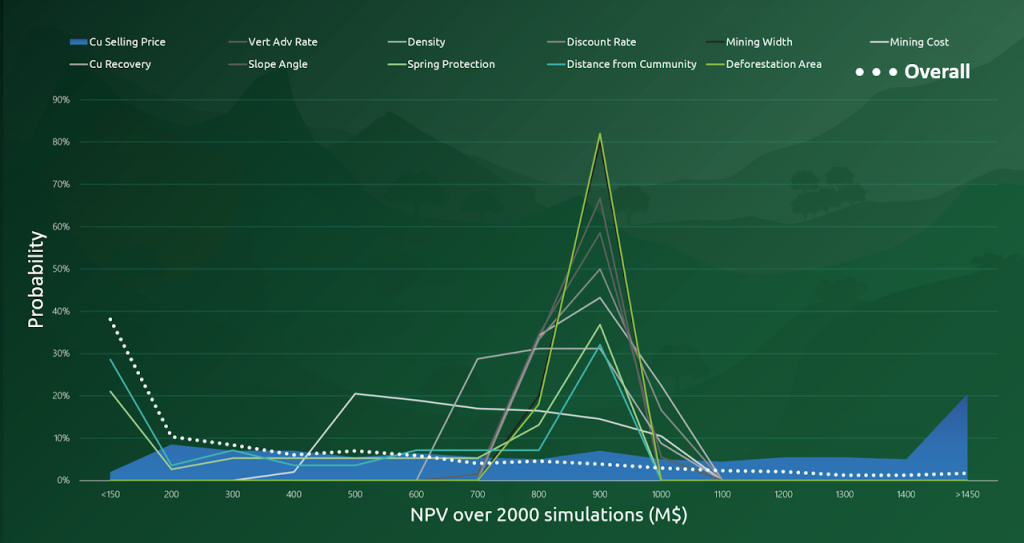
Para comprender mejor los efectos de las restricciones, El equipo de MiningMath llevó a cabo 2,000 simulaciones como se muestra a continuación.
El estudio examinó el impacto de las restricciones individuales y sus efectos combinados..
Variación individual
Las simulaciones iniciales probaron el efecto de variar las restricciones individuales, como el precio de venta del cobre., Anchos de minería, y tasa de avance vertical. Estos parámetros se ajustaron individualmente para comprender sus tendencias.. Los resultados mostraron que la mayoría de las variaciones individuales tenían una alta probabilidad de generar VPN en torno a $900METRO.
Escenarios combinados
La siguiente fase implicó correr "en general" escenarios, donde todos 11 A las variables se les asignaron valores aleatorios simultáneamente. En estos casos, Las restricciones redujeron colectivamente el VPN potencial, con una mayor probabilidad de VPN en torno a $200METRO.
Equilibrar la libertad y las limitaciones
Los hallazgos del estudio anterior resaltan un principio clave: El aumento de las restricciones tiende a disminuir la probabilidad de lograr VPN más altos. Se anima a los usuarios a explorar las limitaciones para lograr un equilibrio entre la libertad del algoritmo y la orientación para lograr resultados prácticos.. A lo largo de la página se dan algunas estrategias para ello..
El equilibrio entre las restricciones y el VPN
- Demasiadas restricciones: Limita la capacidad del algoritmo para explorar el espacio de soluciones., lo que conduce a VPN más bajos.
- Muy pocas restricciones: Proporciona una libertad excesiva, lo que puede dar lugar a soluciones poco prácticas para situaciones de la vida real..
Información sobre el algoritmo de MiningMath
MiningMath emplea programación matemática para maximizar el VPN respetando las restricciones impuestas.

Los usuarios avanzados pueden aprovechar esta capacidad colocando restricciones estratégicamente que guíen al optimizador hacia mejores soluciones..
Por ejemplo, Comenzar con un movimiento/producción total sin restricciones permite una mejor distribución de los desechos a lo largo del tiempo. Después, aplicando límites de producción (p.ej, 100 mtpa, 90 mtpa) Ayuda a evaluar tendencias creando una curva de escenarios contra el VPN.
Gestión de restricciones
El enfoque ideal comienza con restricciones mínimas y gradualmente introduce otras razonables.. Al hacerlo, El algoritmo se centra en un espacio de soluciones más estrecho, potencialmente produciendo VPN más altos.
Flujo de trabajo recomendado
Comience con restricciones mínimas y evite agregar geometrías complejas.
Introduzca gradualmente restricciones una por una para observar su impacto en el VPN.
Utilice un Flujo de trabajo para evaluar cómo cada supuesto influye en los resultados del proyecto a largo plazo.
Medir la "costo" de cada restricción para orientar las decisiones de gestión.
Estrategias de restricción inteligentes
Relajar las restricciones cuando sea posible: Por ejemplo, Flexionar temporalmente los ángulos de pendiente para mejorar los diseños.
Utilice sugerencias para guiar el algoritmo: Relajar las restricciones de baja prioridad o simplificar escenarios complejos en problemas más pequeños.
Iterar gradualmente: Optimizar desde los escenarios menos restringidos hasta los más restringidos.
Enfoque de reestructuración
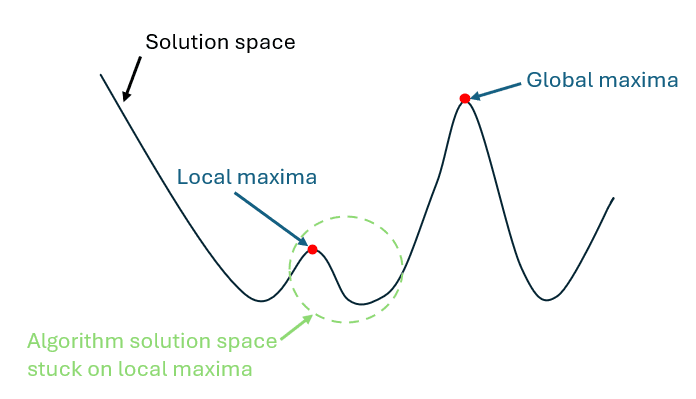
Los problemas de optimización no lineal a menudo presentan desafíos debido a la presencia de máximos locales., donde el algoritmo puede llegar a ser “atascado,” impidiéndole encontrar los máximos globales.
Una estrategia eficaz para mitigar este problema es introducir ligeras modificaciones en los parámetros.. Estos ajustes deben ser lo suficientemente pequeños como para no alterar significativamente el resultado práctico, pero deben ser suficientes para cambiar la estructura matemática del problema..
Algunos ejemplos (no exhaustivo) de las restricciones que podrían ser alteradas son:
- Capacidades de procesamiento: Introducir cambios menores en los límites de procesamiento. Por ejemplo, reduciendo o aumentando la capacidad del molino 1-2% Puede cambiar el equilibrio entre las prioridades de manejo de desechos y procesamiento de minerales..
- Tasa de descuento: Modificar ligeramente la tasa de descuento utilizada en los cálculos del VPN. Esto afecta la forma en que se valoran los ingresos futuros y puede llevar al algoritmo a favorecer diferentes cronogramas de proyectos..
- Parámetros de existencias: Modificar los límites máximos o mínimos de almacenamiento en pequeñas cantidades. Esto puede impulsar al algoritmo a explorar estrategias alternativas de almacenamiento..
- Límite de tiempo: Es posible indicar una límite de tiempo en horas antes de ejecutar un escenario. A pesar de no estar implementado para este propósito, Este parámetro también podría usarse para encontrar soluciones más diversas..
Este “Reorganización” El enfoque alienta al algoritmo a explorar caminos alternativos en el espacio de soluciones., potencialmente evitando los máximos locales y mejorando las posibilidades de identificar mejores soluciones.
Relajado vs.. restricciones violadas
Comprender los matices de las restricciones es fundamental. Las restricciones pueden relajarse para lograr resultados factibles, pero no deben violarse de manera que hagan que el proyecto sea inviable..
Ejemplos de restricciones que podrían relajarse:
- Deficiencias en el flujo de procesamiento.
- Restricciones operativas.
- Ciertas restricciones basadas en promedio o suma (dependiendo de la desviación).
Ejemplos de restricciones violadas
- Límites de producción excedidos.
- Violaciones del ángulo de pendiente.
- Restricciones críticas basadas en promedio o suma que violan la viabilidad.
Los informes que detallan estos matices están disponibles en la salida de Excel. Pestaña de informe para revisión.
Conclusiones clave!
- Explora la libertad primero: Comience la optimización con restricciones mínimas para descubrir el potencial económico de un proyecto.
Introducir la orientación gradualmente: Agregue restricciones cuidadosamente para guiar el algoritmo hacia resultados realistas.
Jerarquía de apalancamiento: Utilizar el orden jerárquico Priorizar y relajar las restricciones estratégicamente.
Resolución iterativa de problemas: Desglosar escenarios complejos e iterar en múltiples ejecuciones para evaluar tendencias.
- “Reorganización” acercarse: Modifique ligeramente sus parámetros para estimular al algoritmo a explorar soluciones alternativas.